
Un ingénieux dispositif mécanique, inspiré de la célèbre « méthode du jardinier », permet de découper une planche de bois selon une ellipse dont la longueur des axes est donnée. Pour tracer une ellipse, la méthode du jardinier consiste à se munir d'une cordelette non élastique et à faire circuler un crayon en maintenant la cordelette toujours bien tendue.
.jpg)
Une ellipse E est par définition l'ensemble des points M dont la somme des distances à deux points fixes (F et F') est constante. Son équation peut s'écrire x2 / a2 + y2 / b2 = 1, avec a la longueur du demigrand axe et b celle du demi petit axe.
L'animation suivante est disponible sur YouTube:
Merci à Grégoire Baudry pour ses remarques sur un dispositif de découpe d'une ellipse exploitant une construction dérivée de ce procédé (figure ci-dessous) où deux points d'une tige sont assujettis à se déplacer sur deux axes perpendiculaires, un autre point de la tige traçant l'ellipse voulue. Lors du mouvement, tous les points de cette tige décrivent des ellipses de centre O, point d'intersection des deux axes.
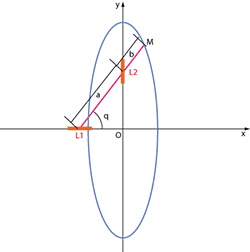
Dans le mouvement le long des axes (Ox) et (Oy), le coulissement des languettes L1 et L2 fait que les longueurs a et b sont constantes. L'abscisse x(M) du point M est égale à b cos(θ), son ordonnée y(M) vaut (a + b) sin(θ). On reconnaît (après rotation de 90°) l'équation d'une ellipse de grand axe a + b et de petit axe b. Cette figure évoque le mouvement d'une bande de papier qui glisse sur un plan, et un chapitre bien oublié de la géométrie, le mouvement plan sur plan. Dans ce type de mouvement, on distingue un plan fixe, P, et un plan mobile, M.
On suppose que les déplacements sont paramétrés par le temps t. Au cours du mouvement, les points tels que A et B décrivent respectivement des courbes CA et CB. Les distances étant conservées dans le mouvement, on passe de la position du plan M(t) à une position infiniment voisine M(t') (où t'=t+dt) par une rotation infinitésimale d'angle dθ autour d'un point I(t), dénommé centre instantané de rotation.
.jpg) Lors du mouvement du plan mobile M(t), la distance entre deux points A et B de ce plan est constante, ce qui indique qu'il s'agit, à chaque instant, d'une rotation.
Lors du mouvement du plan mobile M(t), la distance entre deux points A et B de ce plan est constante, ce qui indique qu'il s'agit, à chaque instant, d'une rotation.
Au cours du mouvement infinitésimal du point A le long de la courbe CA, les normales en deux points voisins A et A' se coupent au centre instantané de rotation, et ceci quel que soit le point considéré. Aussi, les normales à toutes les courbes parcourues par les différents points du plan M se coupent, à un instant t donné, au centre instantané de rotation, ce qui donne une construction facile de ce point, due à Chasles.
.jpg) Une droite (AB), dont le point A se déplace sur CA et le point B sur CB, enveloppe une courbe. Le centre instantané de rotation I est à l'intersection des normales à CA et CB en A et B. Le point caractéristique de contact de la droite (AB) avec son enveloppe est sur la perpendiculaire menée de I à (AB).
Une droite (AB), dont le point A se déplace sur CA et le point B sur CB, enveloppe une courbe. Le centre instantané de rotation I est à l'intersection des normales à CA et CB en A et B. Le point caractéristique de contact de la droite (AB) avec son enveloppe est sur la perpendiculaire menée de I à (AB).
Base, roulante et enveloppe
Le lieu géométrique du centre instantané de rotation dans le plan fixe P est nommé la base B ; le lieu dans le plan mobile M est la roulante R. La roulante R « roule sans glisser » sur la base B, ce qui peut se représenter par une base et une roulante faites de minuscules dents qui s'engrènent au cours du mouvement.
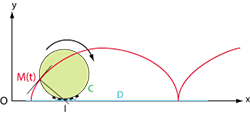
Un point M du cercle C qui roule sans glisser sur une droite D engendre la cycloïde. La normale au point M à la cycloïde passe par le centre instantané de rotation I du mouvement plan sur plan.
Voici un exemple animé disponible sur Youtube :
Ainsi, dans le mouvement d'un cercle C (la roulante) qui roule sans glisser sur une droite D (la base), la trajectoire d'un point M du cercle C dans le plan P est la cycloïde. De nombreuses propriétés de cette courbe ont été déduites au xviie siècle par Descartes, qui utilisa les propriétés liées à ce mouvement, dans une lettre au père Mersenne. Descartes peut être considéré comme le fondateur de ce domaine de la géométrie. D'autres mathématiciens ont étendu le domaine, notamment Michel Chasles (1793-1880, voir Tangente 160) et Gabriel Koenigs (1858-1931). Ce dernier démontra que si trois plans se déplacent l'un sur l'autre alors les trois centres instantanés de rotation des plans pris deux à deux sont alignés.
Le mouvement plan sur plan est utilisé dans la théorie des enveloppes de droites (l'enveloppe d'une famille de droites est la courbe à laquelle toutes les droites sont tangentes). Ainsi, le point dit caractéristique de contact d'une droite avec son enveloppe est déterminé simplement par la construction du centre instantané de rotation à l'aide des normales due à Chasles.
Revenons à notre bande de papier, dont deux points A et B distants d'une longueur l parcourent deux axes perpendiculaires (voir figure I).
À l'instant t, le centre instantané de rotation I(t) est sur la perpendiculaire à (Ox) en B et sur la perpendiculaire à (Oy) en A. Le quadrilatère OAIB est un rectangle, dont les diagonales sont de longueur fixe l : le lieu géométrique du centre instantané de rotation I dans le plan fixe F est le cercle CF de centre O et de rayon l. Ce cercle CF est la base.
Le cercle R(t) de diamètre l et de centre P(t), point de concours des diagonales du rectangle OAIB, est tangent en I au cercle CF. Dans le plan mobile M de la bande de papier, ce cercle est le lieu géométrique du centre instantané de rotation I(t). C'est la roulante du mouvement : le cercle R(t) roule sans glisser sur le cercle CF. Le lieu du point P (t) dans le plan fixe est le cercle de centre Iet de rayon l/2 (figure II).
.jpg) Différents aspects de la cinématique de la bande de papier. (I) Configuration première : lors du mouvement du plan mobile lié à la bande de papier, le point A se déplace selon (Oy) et le point B selon (Ox). (II) L'enveloppe de la droite (AB) est une astroïde. (III) Lors du mouvement de la bande, le point K milieu de [AB] se déplace selon un cercle et le point J selon l'axe des x : cette configuration est dénommée la mouche de la Hire. (IV) Démonstration géométrique qu'un point K de la droite (AB) se déplace le long d'une ellipse.
Différents aspects de la cinématique de la bande de papier. (I) Configuration première : lors du mouvement du plan mobile lié à la bande de papier, le point A se déplace selon (Oy) et le point B selon (Ox). (II) L'enveloppe de la droite (AB) est une astroïde. (III) Lors du mouvement de la bande, le point K milieu de [AB] se déplace selon un cercle et le point J selon l'axe des x : cette configuration est dénommée la mouche de la Hire. (IV) Démonstration géométrique qu'un point K de la droite (AB) se déplace le long d'une ellipse.
Le point J de la figure III, intersection du cercle R(t) avec l'axe (Ox), se déplace sur l'axe (Ox), et K sur le cercle CK. KJ = l / 2. On a construit un engrenage, dit mouche de la Hire, du nom de l'astronome et mathématicien français Philippe de La Hire (1640-1718). Cet engrenage transforme le mouvement circulaire d'un point K en le mouvement rectiligne du point J (une animation est disponible sur en ligne). Il a été très étudié par le passé dans les systèmes bielle-manivelle des locomotives.
Redémontrons géométriquement que le lieu géométrique du point K situé sur le segment [AB] de la bande de papier du schéma IV est une ellipse. Posons AK=α et KB=β. Complétons par le point L le parallélogramme OAKL. Lors du mouvement, le point L se déplace sur le cercle CL de centre O et de rayon α. En appliquant le théorème de Thalés, KE / KL = KE / AO = KA / KB = α / β. Donc le point K se déduit du point L par une affinité orthogonale d'axe (Ox) et de rapport α / β. Le lieu géométrique de K est l'ellipse qui se déduit du cercle CL par cette affinité.
La géométrie est presque complètement absente des programmes, et la cinématique totalement. C'est peut-être dommage : la discipline donnait une intéressante vision dynamique des problèmes géométriques. Notre ministre de l'Éducation nationale veut des mathématiques « qui font sens et ancrées dans le réel ». Le mouvement plan sur plan n'est-il pas une approche « sensée » de la géométrie ?
