Qu'est-ce qu'un tas de sable ? La question a l'air anodine, mais il faut pourtant bien commencer par se la poser ! Pour nos besoins, on versera délicatement du sable fin, sec, homogène sur un support découpé dans du carton rigide et calé horizontalement (la base), jusqu'à saturation. Autrement dit, on ne peut plus déposer le moindre grain de sable sur le tas formé sans que ce grain dévale la pente. La pente a alors atteint une valeur critique, la même en tout point du tas, et c'est ce qui lui vaut d'être appelée surface d'égale pente.
Un sens géométrique très sûr
.jpg)
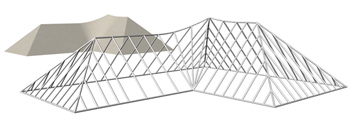
Engageons-nous alors dans une séance de travaux pratiques préparatoires. Découpons dans du carton des supports variés – cercle, carré, rectangle, polygone convexe ou non, formes libres… – et observons. Le cercle produit logiquement un cône de révolution, le carré une pyramide et le rectangle une toiture où les quatre pans ont la même inclinaison. Mais, surprise, si l'on cherche à réaliser à l'identique une toiture constituée exclusivement de surfaces planes couvrant un bâtiment en forme de L, le sable s'y refuse ! Dans l'angle rentrant formé par deux pans de la toiture, le sable continue à s'accumuler jusqu'à former une surface conique (un fragment de cône de révolution) et on voit apparaître une ligne de crête curviligne, réunion de segments de droites et de deux arcs d'ellipses.