
1+ 2 = 2 + 1 : la commutativité de l’addition de nombres réels, c’est-à-dire le fait que l’ordre dans lequel on ajoute les termes n’a aucune influence sur leur somme, semble une évidence. Elle se confirme d’ailleurs empiriquement tous les jours. Pourtant, elle connaît quelques exceptions, qui ouvrent la voie à des possibilités féériques !
Le pouvoir de choisir la somme
Si toute addition comportant un nombre fini de réels est bien commutative (ce sont les cas rencontrés en pratique dans la vie de tous les jours), il existe bel et bien des situations où une addition comportant un nombre infini de termes voit sa somme varier selon l’ordre des termes. Ce sujet, étudié depuis le milieu du XIXe siècle, a été initié par des mathématiciens allemands : Dirichlet semble avoir été le premier à établir que changer l’ordre des termes de certaines séries modifie leur somme ; il a été suivi par Georg Simon Ohm (1789–1854), Bernhard Riemann ou encore Oscar Xavier Schlömilch (1823–1901).

Des critères précis seront découverts par Bernhard Riemann et conduiront au théorème de réarrangement. Bien qu’ayant été un pionnier des mathématiques fécond et influent, célébré notamment en analyse pour les intégrales qui portent aujourd’hui son nom et ses travaux sur la fonction zêta, Riemann a bénéficié de relativement peu de reconnaissance suite à la découverte de ce résultat.
Une intuition extraordinaire
Riemann a établi de manière irréfutable que changer l’ordre des termes de certaines additions (les séries semi-convergentes) a pour implication de… modifier leur somme ! Ses travaux ont permis d’aller encore plus loin encore : s’il était là, Riemann vous affirmerait, tel un magicien : « Donnez-moi n’importe quel réel, ou même plus ou moins l’infini, et je ferai converger cette série vers ce réel ou je la ferai diverger. » Autrement dit, Riemann a compris le premier comment dompter ce genre de séries, en inventant une permutation adéquate des termes afin de faire adopter à la série la somme de son choix. C’est un résultat époustouflant !
Pour comprendre comment Riemann s’y prend, penchons-nous sur son théorème de réarrangement : il y décrit d’abord les suites pour lesquelles s’applique ce résultat, celles qui répondent au critère de semi-convergence (à savoir qu’elles convergent vers un réel r, mais qu’elles divergent en valeur absolue). Autrement dit, la série de terme général un converge et la série de terme général |un| diverge. De manière formelle :
Considérons à présent la série harmonique alternée :
Cette série converge vers l’opposé du logarithme népérien de 2, à savoir –0,693…, mais la série harmonique
elle, diverge.
Les séries qui nous intéressent auront ainsi des termes strictement positifs et d’autres termes strictement négatifs.
La semi-convergence nécessaire à la démonstration du théorème de réarrangement est liée à la possibilité d’avoir à disposition des termes négatifs ou positifs en quantité infinie. Une série semi-convergente possède précisément une alternance de tels nombres. Ensuite, pour que l’intuition de Riemann soit vérifiée, il faut que les deux séries obtenues à partir de S en ne considérant que les termes positifs (d’une part) et négatifs (d’autre part) divergent. Or, ces deux sous-séries divergent effectivement. Pour le voir, notons A = (an)n≥0 la sous-suite de (un)n≥0 constituée uniquement des termes positifs et B = (bn)n≥0 celle des termes négatifs. Reformulons de manière astucieuse les termes généraux des suites A et B :
On a bien an = 0 si un < 0 et an = un si un > 0. Cette égalité implique que la série de terme général an est la somme d’une série divergente à termes positifs et d’une série convergente, donc elle diverge.
De même, pour tout entier n, , et B diverge également comme différence d’une série convergente et d’une série divergente.
Ainsi, toute série semi-convergente possède en quantité infinie des nombres positifs et en quantité infinie des nombres négatifs, et leurs sommes respectives divergent toutes deux.
Réarranger les termes
Prenons la série harmonique alternée et choisissons un réel arbitraire, disons 10100. On souhaite réarranger les termes de la série grâce à une permutation de manière à faire tendre notre série non plus vers –ln (2), mais vers 10100.
Voici l’idée géniale de Riemann : commençons par sommer tous les termes positifs de la série jusqu’à dépasser 10100. Arrêtons-nous dès que 10100 est franchi ; ceci est possible car la série associée A diverge. Faisons maintenant intervenir la série B des termes négatifs, que l’on « déroule » jusqu’à repasser sous 10100 (concrètement, à cette étape, il suffit de considérer le premier terme de la série harmonique, à savoir –1). Reprenons A là où on l’avait laissée et additionnons à nouveau tous ses termes dans l’ordre jusqu’à dépasser 10100. Une fois 10100 dépassé, ajoutons le deuxième terme négatif de B, c’est-à-dire –1/3 : on passe immédiatement sous 10100. Reprenons alors A au terme où on l’avait laissée pour continuer notre algorithme, et ainsi de suite. Aucun des termes de la série harmonique n’est oublié, et chaque terme n’est pris qu’une fois : on obtient donc bel et bien une permutation des termes de la série considérée. La convergence de la nouvelle série issue du réarrangement de termes peut être visualisée comme suit : une ascension vers 10100, puis une oscillation autour de 10100 de « plus en plus resserrée », par au-dessus et en-dessous, en alternance.
Voici, graphiquement, à quoi ressemble le type de suite que l’on construit, avec l’exemple de la série harmonique alternée réarrangée afin de converger vers 3.
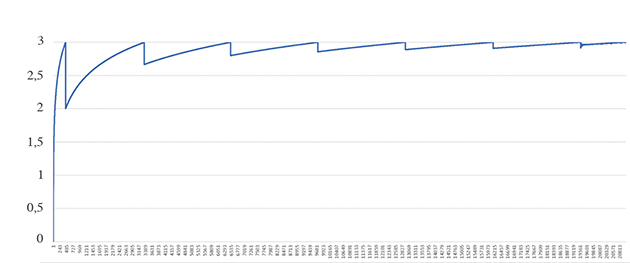
Convergence de la série harmonique alternée réarrangée vers 3.
Cette expérience de pensée fascinante permet d’entrer dans le monde mystérieux de l’infini mathématique. On y croise des ensembles dénombrables (les entiers, les nombres relatifs, les rationnels, les nombres pairs, les carrés parfaits…) et des ensembles indénombrables (les réels, les complexes, les fonctions de [0, 1] dans lui-même…). Le mathématicien allemand Georg Cantor (1845–1918) est à l’origine de cette théorie, qui continue de produire des résultats extraordinairement contre-intuitifs. Ses idées ont d’ailleurs été mal reçues en son temps… Aujourd’hui cependant, plus que jamais, selon les mots de David Hilbert, « nul ne saurait nous chasser du paradis que Cantor a créé pour nous ».
