
À la suite des paradoxes de Zénon, les anciens Grecs s’interdirent le recours à l’infini en ne le concevant, tout comme Aristote, que comme potentiel : on peut partager un segment en morceaux de plus en plus petits, sans que l’opération mentale n’ait de fin théoriquement assignable mais sans jamais pourtant que l’on puisse matériellement la prolonger effectivement à l’infini.
Le recours à l’infini actuel, c’est-à-dire un infini présent « pour de bon », revint en grâce bien plus tard, notamment sous l’impulsion de Bonaventura Cavalieri (1598–1647) et sa méthode des indivisibles qu’il exposa dans Geometria indivisibilibus continuorum nova quadam ratione promota publié en 1635. Celle-ci était cependant déjà utilisée par Gilles Personne de Roberval, comme le Français l’a rappelé en juin 1647 dans une lettre à Evangelista Torricelli (1608–1647, voir FOCUS).
Roberval a utilisé cette méthode pour étudier l’aire sous une arche de cycloïde, cette courbe « star » de l’époque qui a donné aux mathématiciens l’occasion de dépasser les théorèmes de la géométrie classique et de préparer l’avènement du calcul infinitésimal.
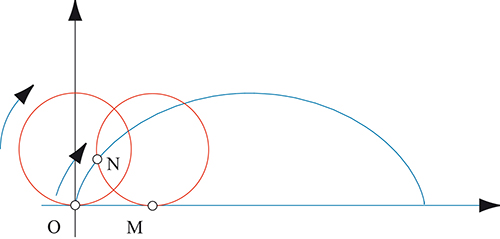
Parce que la roue roule sans glisser, les longueurs OM (mesurée positivement à droite de O) et MN (mesurée sur le cercle tangent au sol en M) sont égales.
Quarrer la cycloïde
La cycloïde est la courbe ...
Lire la suite
