
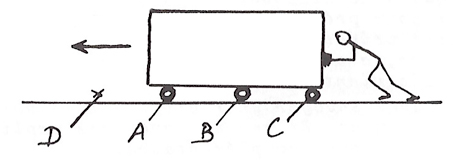
Quand on veut déplacer un objet lourd et volumineux, par exemple un coffre, sur un sol à peu près horizontal, on ménage beaucoup sa peine en plaçant des « rouleaux » entre le sol et l’objet. Comme on le voit sur le schéma, plusieurs rouleaux A, B, C… sont nécessaires. Quand le coffre avance dans la direction de la flèche, le rouleau C échappe vers l’arrière : il faut que quelqu’un vienne le prendre, et aille le placer en avant du coffre (vers D).
Des rouleaux qui ne roulent pas
Les rouleaux limitent les efforts pour déplacer le coffre mais ont un inconvénient : ils roulent très facilement si le sol est en pente… Comment pourrait-on avoir des rouleaux permettant de déplacer un coffre avec le minimum d’efforts, et qui ne rouleraient pas d’eux-mêmes sur un sol en pente ? La figure suivante vous propose un « rouleau à section triangulaire » qui ne roule sûrement pas tout seul. L’ennui, c’est que si l’on pose un coffre sur la pointe C et qu’on le pousse, soit il doit glisser sur la pointe C (et c’est alors aussi dur que si le coffre était posé à même le sol), soit le ...
Lire la suite
