Pour tout ensemble S = { X1, X2… Xn } avec X1 > X2… > Xn > 0, il s’agit de construire un graphe G ayant exactement X1 + 1 sommets et tel que deg(G) = S. La construction se fait par récurrence sur le nombre n d’entiers contenus dans S.
Le cas de base est simple. Soit un ensemble composé d’un seul entier : S = {x}, avec x > 0. Considérons le graphe complet Kx+1. Chacun de ses x +1 sommets est de degré x et voisin des x autres sommets. Kx+1 répond aux attentes lorsque le cardinal de S est 1.
Pour tout ensemble S de cardinal n, on écrit S = {X1, X2… Xn } avec X1 > X2… > Xn > 0. Notre hypothèse de récurrence est qu’il existe un graphe G avec X1 + 1 sommets et deg(G) = S. Prenons maintenant un ensemble T = {Y1, Y2… Yn , Yn+1 } quelconque de cardinal n + 1, avec Y1 > Y2… > Yn > Yn+1 > 0.
Construisons S’ = {Y1 – Yn+1, Y1 – Yn … Y1 – Y2 } à partir de T. On a Y1 – Yn+1 > Y1 – Yn >… > Y1 – Y2 > 0 ; S’ est donc un ensemble de n entiers positifs. Par hypothèse de récurrence, il existe alors un graphe H à Y1 – Yn+1 + 1 sommets vérifiant deg(H) = S’. Ajoutons à ce graphe H un ensemble C de Yn+1 nouveaux sommets, sans aucune arête. Le graphe ainsi obtenu, noté H+, possède Y1 – Yn+1 + 1 + Yn+1 = Y1 + 1 sommets.
Pour obtenir le graphe G recherché, il suffit de considérer le complémentaire du graphe H+. Quelles sont les caractéristiques de G ? Comme H+, il a Y1 + 1 sommets. Calculons-en les degrés. Par construction, chacun des Yn+1 sommets de C est connecté à tous les autres sommets de G, c’est-à-dire à Y1 voisins. G contient bien au moins un sommet de degré Y1.
Montrons que pour tout j dans {2, 3… n+1} G contient aussi au moins un sommet de degré Yj. Le graphe H (donc H+) contient au moins un sommet u de degré Y1 – Yj . Dans le complémentaire G, ce sommet u est voisin des Y1 + 1 sommets sauf u lui-même et ses « anciens » Y1 – Yj voisins.
Le degré de u dans G est donc Y1 + 1 – 1 – ( Y1 – Yj ), soit Yj .
Pour conclure, il reste à constater que G ne contient aucun sommet ayant un degré hors de T. Le graphe G a donc bien toutes les caractéristiques demandées !
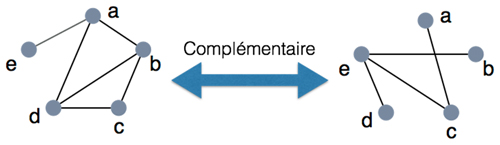
Le complémentaire d’un graphe
Pour tout graphe H, le complémentaire G de H est le graphe défini de la manière suivante. G possède exactement les mêmes sommets que H et, pour toute paire {u, v } de sommets, si H contient une arête entre u et v alors G n’en contient pas et si H ne contient pas cette arête alors G la contient.