La puissance du raisonnement mathématique se révèle parfois d’un réconfort solide, même dans les domaines les plus inattendus. Face aux ravages du Covid-19, en des temps difficiles et incertains, une représentation rationnelle, fondée sur des hypothèses réalistes, apporte des réponses argumentées à certaines des questions que chacun se pose. Même si personne ne peut appréhender toutes les conséquences sociétales et économiques de la pandémie qui sévit en ce moment, le recours à la modélisation du phénomène s’avère d’un apport considérable, en expliquant ou en justifiant certaines mesures prises, comme le confinement ou la mise en quarantaine. Certes, le recours à la modélisation, et donc à une forme de simplification, se fait toujours par le biais d’une série d’hypothèses simplificatrices dont la validité n’est pas nécessairement acquise. Il convient d’en tenir compte au moment des conclusions et lors de la phase de décision. C’est encore plus vrai pour un phénomène épidémiologique comme le Covid-19, pour lequel des données fiables ou exhaustives sont encore aujourd’hui pratiquement indisponibles.

Le modèle SIR
Plusieurs modèles épidémiologiques ont été développés à ce jour. Les plus élémentaires sont les modèlescompartimentaux, qui apportent déjà un éclairage particulièrement intéressant sur certains aspects du phénomène pandémique que nous vivons en ce moment. Le modèle SIR appartient à cette catégorie.
Considérons un groupe d’individus constituant une certaine population P d’effectif n, avec n « grand ». Dans un premier temps, on suppose la totale absence d’immunité initiale dans P. C’est bien le cas en ce qui concerne le Covid-19 : aucun vaccin n’était déjà disponible au moment de son apparition, et les systèmes immunitaires des personnes concernées, non confrontées au virus nouveau, n’avaient pas encore été à même de réagir. On suppose aussi tous les individus « semblables ». Cette hypothèse n’est évidemment pas vérifiée en pratique mais, le raisonnement se faisant sur une population large, un traitement en moyenne ne peut être inintéressant.
On partage la population en trois groupes. Il y a d’une part les personnes saines, S (comme « susceptibles »), d’autre part les personnes infectées, I (comme « infectious »). Enfin, il y a le groupe des personnes guéries, R (comme « recovered »). Le tout donne naissance à l’acronyme SIR.
Le compartimentage peut évidemment être plus subtil. On peut en effet ajouter une catégorie de décédés, D (comme « dead ») et un groupe des personnes infectées mises en quarantaine, Q, qui, de ce fait, n’ont plus d’action négative sur la population saine. Dans un premier temps, il est surtout question de visualiser l’évolution de la situation des infections lorsque aucune mesure n’est prise et que l’on laisse le virus se propager librement.
Les modèles SIR peuvent être discrets ou continus. Dans un cadre discret, on relève, toutes les unités de temps (jours ou semaines), les états des différents compartiments. À l’instant 0, la répartition de la population est supposée connue, avec S de cardinal n − 1, I contenant 1 individu et R vide. On suppose alors qu’à chaque intervalle de temps, tout individu infecté peut contaminer toute personne du compartiment S avec une certaine probabilité p. Après chaque unité de temps, un individu infecté se trouve guéri (ou mort) et passe donc de I à R (ou à D). Le modèle est donc stochastique et peut potentiellement déboucher sur un grand nombre de cas de figure. Pour rendre compte de l’évolution des compartiments, l’Institut international de la statistique (ISI, organisation créée en 1885 et indépendante de tout gouvernement) a diffusé, à l’attention de tous ses membres, un excellent exposé sur le sujet réalisé par le professeur Tom Britton (Université de Stockholm) et disponible en ligne. Ce statisticien a mis en place un processus de simulations de grande ampleur, prenant en compte différentes valeurs du couple (n, p). L’un des paramètres du modèle va se révéler fondamental au niveau des conclusions tirées : c’est le taux de reproduction de base, à savoir, le nombre de personnes de P que chaque personne malade peut infecter. Britton estime ce paramètre au départ par la relation approximative R 0 ≈ (n − 1) p ≈ np, en jouant sur la taille de P d’une part, sur la petitesse de p d’autre part.

Le mathématicien Tom Britton.
Deux cas de figure majeurs vont se présenter. Lorsque R 0 est inférieur ou égal à 1, aucune épidémie ne se déclare. Le taux de personnes contaminées ne dépasse jamais 10 %. Par contre, dès que le taux de reproduction de base R 0 dépasse 1, deux scénarios apparaissent. Soit le virus disparaît rapidement, contaminant un petit nombre d’individus (moins de 10 %), soit un pourcentage critique de contaminés est observé. Ainsi, pour R 0 = 1,5, on observe, dans une grande quantité de simulations, un taux de contamination voisin de 60 %. Par contre, des valeurs intermédiaires entre 10 et 50 % de contamination ne sont jamais observées. Ce phénomène peut s’expliquer. En effet, notons τ le taux final de personnes infectées par la pandémie. Le nombre total d’individus ayant transité dans la catégorie I est donc égal à nτ. La proportion non infectée par le virus dans la population est évidemment 1 − τ. Dans le cadre du modèle, on peut voir cette quantité comme une probabilité, en fait la probabilité de n’avoir pas été infecté par les nτ individus eux-mêmes porteurs du virus durant toute la durée de l’épidémie. Si les contaminations sont des évènements indépendants, on peut noter 1 − τ = (1 − p) nτ.
Il reste encore à remplacer p par sa valeur induite à partir du taux de reproduction de base estimé, à savoir p = R 0 / n. On obtient donc la relation qui possède une limite bien connue lorsque n tend vers l’infini, exp (− R 0τ).
L’estimation du R0
L’équation à résoudre est donc 1 − τ − exp(−R 0τ) = 0. Notons f (τ) le membre de gauche. L’équation possède toujours la solution triviale τ = 0. C’est d’ailleurs la seule solution pour toute valeur de R 0 inférieure ou égale à 1. Par contre, pour des valeurs R 0 strictement supérieures à 1, une deuxième solution positive apparaît, comme on le voit sur le graphique suivant, qui représente la fonction f (τ) correspondant à la valeur R 0 = 1,5.
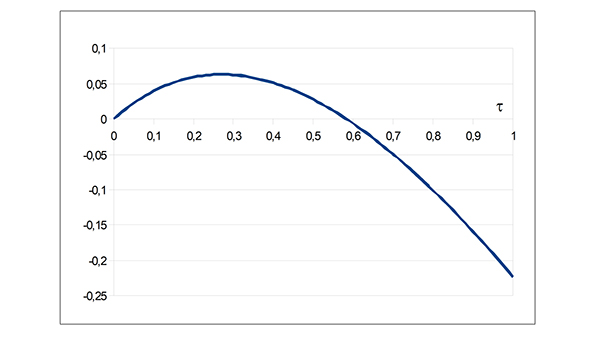
Représentation de la fonction f pour R0= 1,5.
La seconde solution (τ ≈ 58 %) est en parfait accord avec les résultats observés lors de la simulation. Il n’y a pas de forme explicite pour la solution générale mais les calculs numériques se font aisément et livrent le graphique suivant, donnant une estimation du taux de contamination τ de la population en fonction du taux de reproduction de base R 0. La croissance est « rapide » dès que R 0 s’éloigne de la valeur pivot 1. Dans le cas du Covid-19, diverses sources estiment la valeur du paramètre R 0 entre 2 et 2,5, ce qui, sans réaction de la population et prises de mesures préventives, laisse entrevoir un taux de contamination de l’ordre de 80 %.
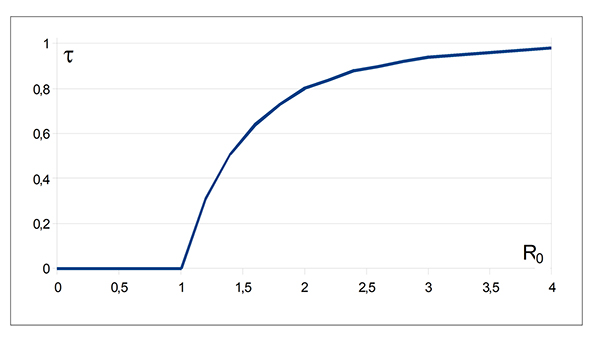
Estimation de τ en fonction de R0.
Le modèle continu
Le modèle SIR se prête également à une description continue. La vitesse à laquelle le virus se propage rend cette description également intéressante. Notons S(t), I(t) et R(t) les fonctions quantifiant les effectifs des trois groupes S, I et R à un instant t ≥ 0. Pour une population de taille n, on pose
En effet, les variations de population saine (via le nombre de nouveaux malades) sont proportionnelles à la population saine et à la population d’infectés. La propagation se fait au taux β.
De même, on suppose que le nombre de nouveaux guéris sera une fraction du nombre d’infectés :
Enfin, la variation du nombre d’infectés sera affectée positivement par l’apport de nouveaux malades et négativement par la proportion de guéris :
Le modèle est non linéaire mais des solutions numériques peuvent être obtenues par simulation. En sommant les trois équations différentielles, on obtient 0, ce qui implique que la somme S + R + I est, à chaque instant t ≥ 0, constante et égale à la taille n de la population. Ceci implique également qu’il suffit de résoudre deux des trois équations d’évolution.
On introduit également un taux de reproduction de base, qui est estimé à partir du ratio β / γ, et que l’on peut interpréter comme le rapport entre taux de contamination et taux de guérison. Des solutions explicites pour S(t) peuvent alors être obtenues, comme dans le cas discret.
L’effet des mesures
La situation est évidemment totalement différente dès que la population touchée comprend une partie d’individus soit immunes, soit vaccinés. Supposons ainsi qu’une proportion q de la population soit immunisée ou vaccinée. Seule la proportion 1 − q de la population pourra être soumise à contamination et subira les effets des individus malades. Notre équation devient à présent 1 − τ = q + (1 − q) exp(− R 0τ).
Imaginons à présent que la moitié de la population soit vaccinée (q = 1/2). La seule solution à la nouvelle équation, pour des valeurs de R 0 inférieures ou égales à 2, est alors la valeur τ = 0. On retrouve de manière quantitative, par le modèle, qu’une vaccination massive est la solution pour éviter un retour du virus et une seconde pandémie. Le graphique suivant compare les situations sans vaccination (en bleu) et avec vaccination (en rouge) pour q = 0,5.
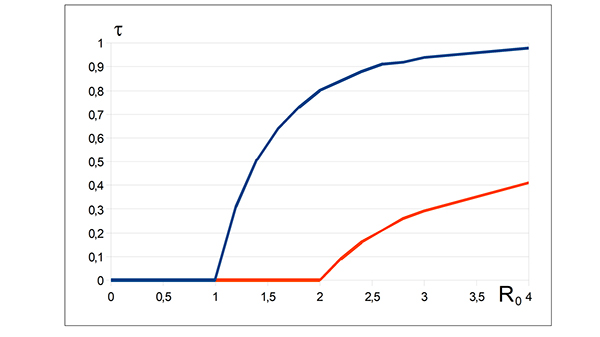
Évolution de τ en fonction de R0, avec (en rouge) et sans (en bleu)
vaccination massive de la population.
Nous n’en sommes pas encore là. Alors ? Que faire pour lutter contre ce qui paraît à première vue inévitable ? Il semble réaliste de supposer que le taux de reproduction basique doit être proportionnel à la probabilité de transmission par contact. C’est le cas dans le modèle SIR précédent : R 0 = np. On peut agir sur cette probabilité en portant des masques, en se lavant les mains, toutes actions qui auront un effet sur le facteur p.
Mais le taux de reproduction dépend tout aussi évidemment du nombre de contacts de chaque individu avec tout autre. On peut donc jouer une seconde fois sur le paramètre R0 en confinant une grande partie de la population à domicile, en interdisant les réunions et rassemblements publics.
D’autres facteurs interviennent également, comme le taux de dépistage dans la population. Dans le cas du Covid-19, certains pays procèdent à un dépistage massif, comme l’Allemagne. D’autres, comme la Belgique, n’ont testé dans les premières semaines que les patients dans un état préoccupant et présentant les symptômes de la maladie, ou encore le personnel soignant… à condition qu’il soit fiévreux ! La taille des populations S et I est donc inconnue. La détermination d’un taux de décès crédible est donc impossible. Le compartiment R reprend donc aussi bien les personnes guéries que les personnes décédées. Des statistiques ultérieures permettront sans doute de quantifier correctement le taux de décès. On constate ici l’intérêt de démarches comme celle du projet Polymath.
Que retenir de tout cela ? Déjà, que des mesures adaptées peuvent être prises et qu’elles doivent jouer sur le taux de reproduction de base. L’intérêt des modèles mathématiques est là : ils quantifient les conséquences de nos actions. En tant qu’outils d’aide à la décision, ils justifient certaines mesures difficiles. Ils nous rassurent enfin quant à l’avenir. Que demander de plus ?
