
Tangente : Professeur Penrose, merci d’avoir accepté de répondre à nos questions. À Tangente, nous nous réjouissons que vous ayez reçu le prix Nobel de physique 2020, conjointement avec deux physiciens !
Sir Roger Penrose : Merci ! Ce prix semble faire plaisir aux mathématiciens. J’y trouve une certaine ironie : le prix m’est décerné pour avoir découvert que « la formation des trous noirs est une prédiction robuste de la théorie générale de la relativité ». Mais là n’est pas ma découverte ! Ce que j’ai montré, c’est que les singularités [voir article « Les singularités en relativité générale »] sont une prédiction robuste de la théorie générale de la relativité. Et vous avez besoin de la « censure cosmique » [voir article « Les singularités en relativité générale », § C'est cosmique !] pour affirmer que vous parlez de trous noirs.
Au sujet de la censure cosmique, maintenez-vous vos conjectures en l’état ou souhaitez-vous les revisiter ?
Il existe des singularités non génériques, du genre temps. Dans sa forme forte, la conjecture de la censure cosmique énonce que les singularités génériques sont du genre espace. Je pense encore que c’est vrai, mais je n’ai toujours pas de preuve !
Sous les pavés, le pavage
Nous aimerions revenir sur vos travaux relatifs aux pavages apériodiques. En 1973, vous avez trouvé six tuiles permettant de forcer un pavage apériodique. Comment avez-vous réussi à réduire leur nombre à 4, puis à 2 ?
Ha ha ! Je peux vous raconter l’histoire… J’ai commencé avec le découpage du pentagone. J’étais invité à donner une conférence à l’un des colleges qui faisait partie de l’université de Londres. En répondant à leur lettre, j’ai remarqué que leur logo, dans le coin, était un pentagone subdivisé en six pentagones plus petits : un dans chaque coin, un au milieu. Il y a des vides, de forme triangulaire, entre les pentagones.

Le logotype de l’université de South Bank de Londres.
Je me suis alors essayé à itérer cette procédure de subdivision des pentagones, encore et encore. Les vides se multipliaient ; je devais choisir comment les remplir. J’y ai mis des pentagones. Les espaces résiduels étaient alors des losanges et des décagones étoilés, à savoir des pentagrammes sans les traits intérieurs. J’ai appelé demi-pentacle la partie centrale avec trois « pointes », ce qui représente plus qu’un demi-pentagramme, au sens strict. Avec les losanges, c’était ce dont j’avais besoin pour définir un motif non répétitif. J’ai su plus tard qu’un Japonais avait fait quasiment la même chose que moi, un peu avant moi je crois, mais il a fait un autre choix, infructueux, de remplissage des espaces résiduels.
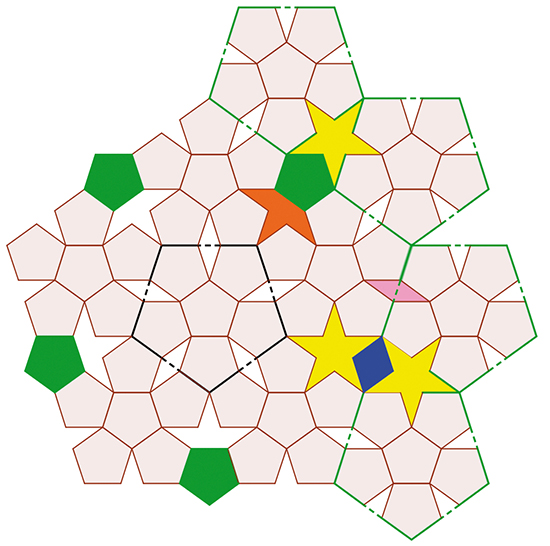
Le grand pentagone est subdivisé en six pentagones plus petits, chacun comprenant lui-même six plus petits pentagones. Dans les espaces laissés vides, on peut insérer, au choix : de nouveaux pentagones (en vert), des « demi-pentacles » (en orange) et deux types de losanges (en bleu et en violet).
Plus tard, j’ai vu que l’on pouvait construire un puzzle. [C’est la raison pour laquelle Roger Penrose a fait breveter ces tuiles.] Tout ce dont j’avais besoin pour les pièces, c’était trois versions différentes du pentagone : le pentagone entouré de cinq autres, le pentagone entouré de trois autres, le pentagone entouré de deux autres. [Sur le schéma, effectivement, chaque pentagone partage un côté avec soit deux, soit trois, soit cinq pentagones.] Il y a des règles d’assemblage naturelles, qui forcent la configuration. [Les règles d’assemblage, ou règles locales, sont de deux types : figurer des courbes colorées sur les tuiles, ou modifier les côtés des tuiles, en les courbant ou en leur ajoutant des pointes et des encoches.] Je disposais alors d’un pavage apériodique constitué de six pièces : les trois versions du pentagone, le demi-pentacle et les deux losanges.
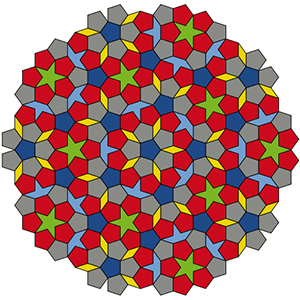
Pavage apériodique du plan avec les six tuiles originales de Penrose.
Une conjecture démontée
J’avais entendu parler d’un article de Raphael Robinson [en 1971], sur le problème de décision de Hao Wang : on se donne des carrés dont les côtés sont colorés et il faut les assembler pour paver le plan de telle manière que les couleurs coïncident bord à bord. Existe-t-il un algorithme pour décider si un pavage du plan est possible avec ces pièces ? Wang avait émis la conjecture suivante : tout ensemble de tuiles qui pave le plan peut le paver de manière périodique. Si elle est vraie, alors il existe un algorithme pour déterminer si un ensemble fini de tuiles peut ou non paver le plan. Or, l’un de ses étudiants, Robert Berger, a montré qu’il ne pouvait exister de telle procédure de décision. [La réponse au problème de décision de Wang est donc négative.] Une partie de l’argument de Berger consistait à montrer qu’il existe un ensemble fini de N tuiles qui ne peut paver le plan que de manière non périodique. Berger l’avait prouvé pour N > 100, Robinson a montré que N = 6 convient.
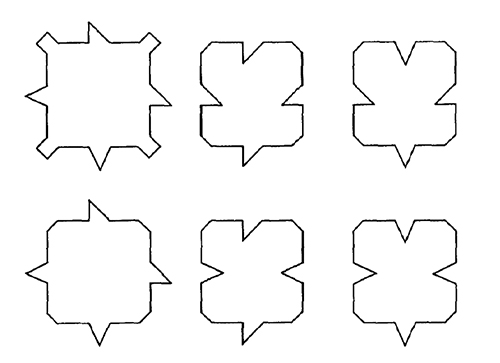
Les six pièces de Raphael Robinson qui permettent
de paver le plan de manière apériodique.
Moi je savais le faire avec N = 5 : la configuration particulière des six pièces me permettait d’en assembler trois pour en créer deux nouvelles, et donc me débarrasser de l’une d’elles. Mais pouvais-je faire mieux ? En peu de temps, j’ai su faire avec quatre tuiles. Pouvais-je encore faire mieux ? J’ai réussi à descendre à deux tuiles, en réarrangeant, découpant et disséquant les quatre formes précédentes. Ma réaction a été : « C’est ridicule, quelle déception, c’est si simple, ça doit déjà être connu ! » Et pourtant…
J’avais deux ensembles de N = 2 tuiles qui convenaient. Le premier que j’ai trouvé, c’est le cerf-volant et la flèche. Les obstructions sont assez évidentes : il ne faut pas emboîter une flèche dans le cerf-volant, mais deux. Ensuite, je suis arrivé aux deux losanges. Pour ce dernier, si vous n’avez pas les bonnes règles d’assemblage, rien ne vous explique ce qui va forcer le caractère apériodique du pavage.
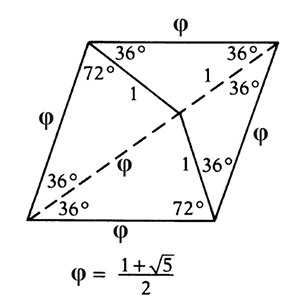
Construction du cerf-volant et de la flèche à partir d’un losange d’angles 72° et 108°.
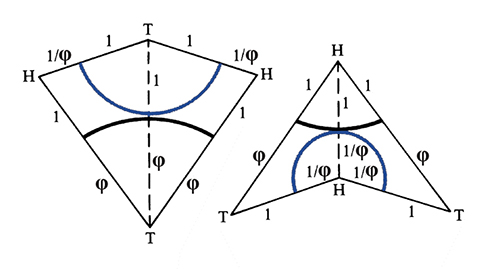
Les règles d’assemblage des deux tuiles pour forcer l’apériodicité du pavage : toutes les courbes doivent être monochromes (il ne faut pas qu’une courbe dessinée sur le pavage soit constituée de morceaux des deux couleurs, noir et bleu).
Les deux tuiles en forme de losange, avec les règles d’assemblage.
Des défis à relever
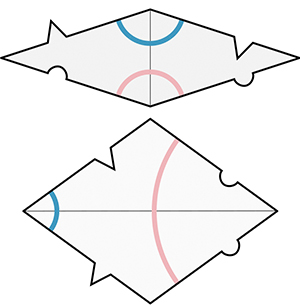
J’ai montré la version originale et une version « en forme d’oiseau » de mes deux tuiles préférées, le cerf-volant et la flèche, à John Conway ; il aurait lui-même adoré trouver ces formes. Il a ensuite passé plusieurs jours, je pense, à en parler avec Martin Gardner, ce qui a conduit à un article dans le Scientific American [Extraordinary non-periodic tiling that enriches the theory of tiles, Scientific American 236, janvier 1977].
Le mathématicien amateur Robert Ammann a ensuite écrit à Gardner : il avait obtenu, indépendamment, et d’une manière complètement différente, le pavage apériodique avec les deux losanges ! Le pavage apériodique d’Ammann–Beenker montre une symétrie de rotation d’ordre 8 [le pavage est invariant par rotation d’angle 2π / 8 radians, soit 45°]. La vraie question est : avait-il trouvé un pavage apériodique possédant une symétrie de rotation d’ordre 5 ?
La version « en forme d’oiseau » du pavage apériodique de Penrose
(symétrie de rotation d’ordre 5).

Le pavage d’Ammann ? Beenker (symétrie de rotation d’ordre 8).
C’est étonnant de ne pas trouver ces pavages dans l’art, ou chez les géomètres du passé…
Mon père avait un ouvrage qui compilait deux livres de Kepler. Dans cet ouvrage sont représentés [dans Harmonices Mundi, 1619] plusieurs formes non cristallographiques, et plusieurs pavages différents. La plus grande image, appelée Aa par Kepler, est un assemblage de pentagones. J’avais vu ce motif, mais ne m’en étais pas souvenu. Dans mon esprit, sans doute, l’idée s’était formée que l’étude des pentagones n’est pas une perte de temps, qu’il y a encore des choses à faire avec.
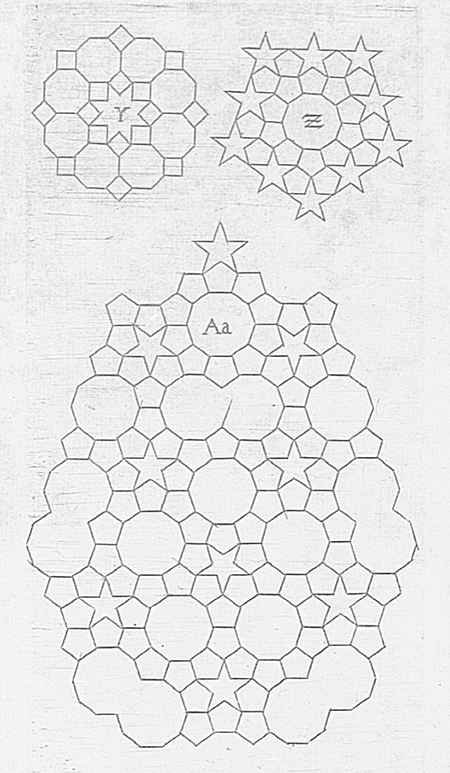
La figure Aa, qui se trouve dans Harmonices Mundi, de Kepler.
Un jour, j’étais en visite à Berne, en Suisse. À cette époque, il y avait un grand intérêt dans les quasi-cristaux. [Daniel Shechtman recevra d’ailleurs le prix Nobel de chimie en 2011 pour ses travaux sur les quasi-cristaux menés à cette époque.] Robert Ammann avait trouvé un pavage apériodique avec une symétrie de rotation d’ordre 8, il y avait ceux d’ordre 10, et ceux d’ordre 5. Hans-Ude Nissen m’annonce alors qu’il croit avoir trouvé un pavage apériodique doté d’une symétrie de rotation d’ordre 12. Il me montre ses images. Il y avait un spectrogramme, avec des points isolés représentant un phénomène de diffraction. Les points sont disposés de manière symétrique et présentent une symétrie de rotation d’ordre 12. Un maillage en arrière-plan permet de dessiner un réseau de triangles et de carrés. Je me suis demandé où je pouvais avoir déjà vu ça. C’était dans l’ouvrage de Kepler ! La figure Ff représente exactement cette disposition des points : un dodécagone avec des triangles pointant vers l’intérieur, d’autres pointant vers l’extérieur, avec des carrés logés entre deux triangles. Nissen avait bien découvert un pavage apériodique avec une symétrie de rotation d’ordre 12, mais personne ne voulait le croire…

La figure Ff, qui se trouve dans Harmonices Mundi, de Kepler.
D’autres questions restent ouvertes sur les symétries des pavages apériodiques et les ensembles minimaux de tuiles permettant de les générer…
Oui. On connaît donc des pavages apériodiques d’ordre 5, 8, 10 et 12. Pour l’ordre 12, on utilise trois tuiles, un dodécagone régulier, un carré, un hexagone avec des marques pour forcer l’apériodicité. [D’autres ensembles de trois tuiles peuvent convenir, un carré, un triangle, un losange par exemple.] Je ne sais pas si l’on peut créer un pavage apériodique d’ordre 12 avec deux tuiles seulement. Voilà une question intéressante !
Du côté de l’intelligence artificielle (IA), on peut se demander : ces pièces étant données, sans aucune autre information, une IA peut-elle deviner les règles qui forcent un pavage apériodique ? C’est facile à programmer car les tuiles se situent sur un réseau hexagonal, contrairement à des pentagones ; il faut simplement décider quelles pièces on place autour du dodécagone, et dans quel ordre. Je serais curieux de savoir si l’IA bloquera assez rapidement ou si elle parviendra à trouver une manière de poursuivre indéfiniment le pavage. Je suis sûr que les outils automatiques de reconnaissance de formes ou de motifs ne sont d’aucune aide ! La technique de construction du pavage consiste en effet à partir d’une des trois pièces, à la découper de manière à faire apparaître uniquement ces trois pièces données, à « zoomer », puis à recommencer, allant ainsi « de l’extérieur vers l’intérieur ». [C’est le processus de déflation/inflation décrit dans l'article « Les singularités en relativité générale » au § La dualité déflation-inflation.] Si l’on demande à l’IA d’aller « de l’intérieur vers l’extérieur », d’assembler méthodiquement le pavage à partir des pièces, je ne suis pas sûr qu’elle ira bien loin…

Pavage apériodique de Penrose à l’entrée du département de mathématiques, à Oxford (Grande-Bretagne), à l’aide de deux tuiles en losange. Les lignes courbes représentent les contraintes imposées par les règles d’assemblage.
Ou encore, prenez le pavage avec des losanges à l’entrée du bâtiment Andrew-Wiles, à Oxford. C’est un pavage dont je suis assez fier, qui n’apparaît nulle part ailleurs. Les lignes courbes serpentent et produisent quatre formes fermées : des cercles parfaits, des « doubles cercles » [on en voit un dans le sens de la hauteur, sur le côté droit de l’image], des « grands décagones arrondis » [on en devine un en bas à droite, qui sort largement de l’image], et un « pentagone arrondi » [la « petite fleur à cinq pétales » au centre de l’image]. Trouve-t-on d’autres courbes fermées, qui ne se recoupent pas, dans ce pavage ? Je pensais que non. Puis j’ai découvert une cinquième forme fermée, très compliquée, qui m’a fait changer d’avis. Je conjecture maintenant que « presque toutes » les courbes qui apparaissent sur ce pavage sont en fait fermées !
Et personne n’a encore apporté une solution à la « conjecture ein Stein ». Je ne pense pas que ce soit impossible qu’une telle forme existe…
