
Newton ou la fabrique de suites performantes
Newton propose son algorithme vers 1669 dans De analysi per aequationes numero terminorum infinitas, et la publie en 1671. Les hypothèses pour appliquer la méthode sont assez restreintes : si f est continue, dérivable deux fois et que ses dérivées première et seconde sont continues autour de la solution et si en outre la dérivée première ne s'annule pas en
, alors la suite définie par
converge vers .
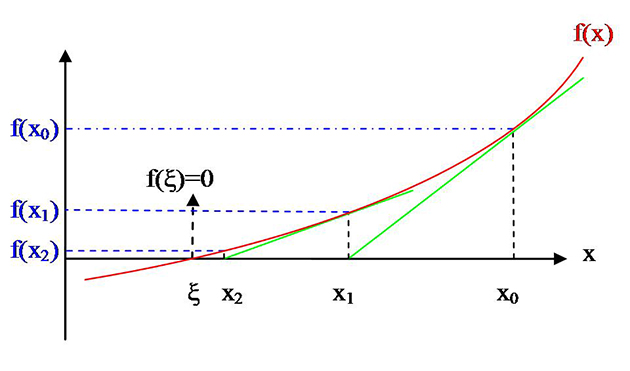
Comme la dérivée f '(x) quantifie la pente de la tangente en x à la courbe de f , l'idée de base est de remplacer une évaluation de la solution xi par l'intersection de la tangente en xi à la courbe et de l'axe des abscisses. Cette évaluation est toujours plus près de la solution ! La méthode de Newton possède de nombreux avantages : sa simplicité, sa facile mise en œuvre, sa convergence ultra rapide, et sa stabilité numérique.
Méthode de Newton : détails des calculs
• La méthode de Héron se déduit de celle de Newton :
Définissons On cherche la solution de f (x) = 0 ; la solution est bien
Or, et
On pose donc
Le tour est joué !
• On peut se passer de la division dans la méthode de Newton :
Posons . Il vient que
. On en déduit que
On est donc conduit à définir
La division a disparu !
Le calcul à la main des racines
Depuis l'arrivée des calculettes, on calcule instantanément des racines carrées. Auparavant, on utilisait un procédé qui ressemblait à une division et que les anciens apprenaient encore à l'école.
On commence par grouper les chiffres du radicande (le nombre dont on cherche la racine carrée) par deux, en commençant par la droite. Dans notre exemple, soit à trouver la racine de 163. Le premier groupe est 63, le suivant est 1. On cherche le plus grand entier dont le carré est inférieur ou égal au groupe de gauche. C'est 1 car 12 = 1 est bien inférieur ou égal à 1, et 22 = 4 > 1. Donc a = 1, on le pose à droite de la barre verticale. Soustrayons a2 à notre tranche, on obtient 1 – 1 = 0. Abaissons la tranche suivante de deux chiffres.
.jpg)
On cherche maintenant le plus grand entier b tel que [2a]b × b soit inférieur à 63 (où le nombre [2a]b est construit en accolant b derrière 2a).
.jpg)
On trouve b = 2. Soustrayons [2a]b × b (ici 44) au reste précédent 63 ; on obtient 19. Posons notre b (égal à 2) à droite du 1. Il n'y a plus aucune tranche de deux chiffres à abaisser, donc pour calculer une décimale, on abaisse après 19 une tranche de deux zéros. De même que pour b, recherchons maintenant le plus grand entier c tel que [2ab]c × c soit inférieur à 1 900.

On trouve c = 7. Retranchons 1 729 à 1 900, il reste 171.
Par le même procédé, recherchons la deuxième décimale d. Ce sera le plus grand entier tel que [2abc]d × d soit inférieur à 17 100 (égal au reste 171 auquel on a ajouté une tranche de deux zéros). On trouve d = 6. On peut continuer ainsi autant que nécessaire : les décimales tombent les unes après les autres, goutte à goutte. Au final, .
Ce processus manuel est long et nécessite de ne pas commettre d'erreurs de calculs (les nombres à manipuler deviennent vite gigantesques), mais il est remarquablement efficace !
