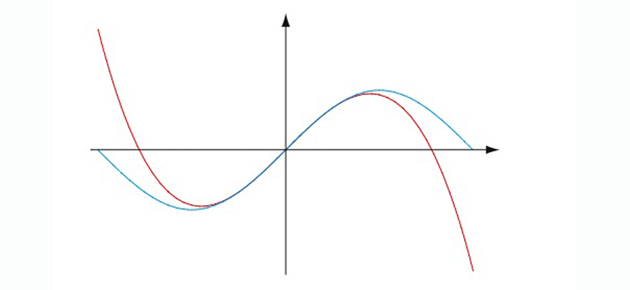
Le problème de l'interpolation polynomiale est le suivant : on connaît une fonction par ses valeurs y0, y1, y2… yN en un certain nombre N + 1 de points x0, x1, x2… xN, et on cherche un polynôme P prenant les mêmes valeurs aux mêmes points, c'est-à-dire tel que P(xi) = yi pour tout i compris entre 0 et N.
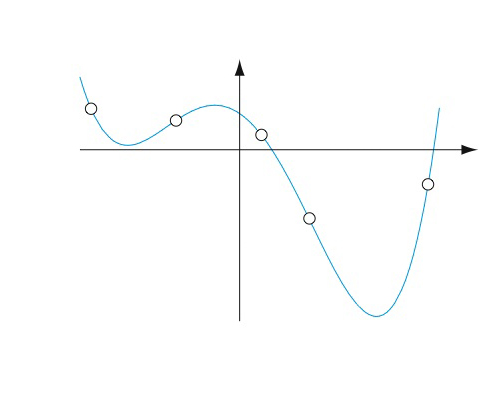
Par cinq points, il passe une et une seule courbe dont l'équation est un polynôme de degré au plus 4.
La condition se traduit par autant d'équations qu'il y a de points, donc N + 1. A priori, P peut être déterminé de façon unique s'il correspond au même nombre de paramètres, ce qui se produit si l'on impose à P d'être de degré au plus égal à N (le nombre de points, moins un). En effet, la question équivaut alors à un système linéaire ayant autant d'équations que d'inconnues à résoudre, ce qui, sauf cas exceptionnel, admet toujours une solution unique.
Afin d'être plus concret, considérons trois points distincts (x0, y0), (x1, y1) et (x2, y2), et cherchons un polynôme du second degré, sous la forme P (x) = ax2 + bx + c, tel que P (x0) = y0, P (x1) = y1 et P (x2) = y2. La question revient à résoudre le système suivant :
Un calcul algébrique fastidieux mais élémentaire montre que ce système de trois équations à trois inconnues a une solution ... Lire la suite
