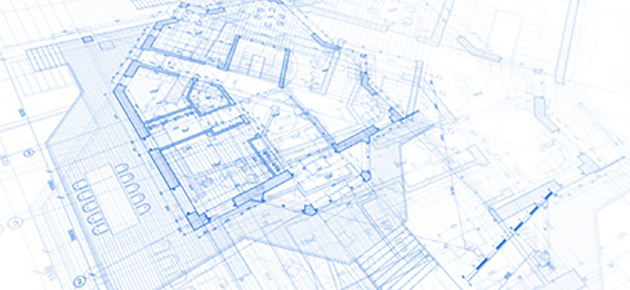
La plus simple des rotations consiste sûrement à effectuer un demi-tour. Plaçons-nous dans le plan complexe d'origine O et considérons un point M d'affixe z = x + iy. Son image M' par la rotation de centre O et d'angle π radians (ou 180 °) a pour affixe z' = –x – iy. On a donc z' = –1 × z.
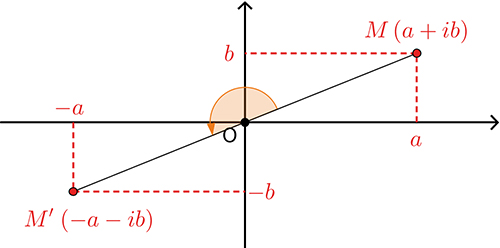
Et pour effectuer un quart de tour seulement ? Existe-t-il un nombre a tel que cette rotation soit décrite par une relation du type z' = az ? Si c'est le cas, on aurait a2 = – 1. En effet, appliquer deux fois une rotation d'un quart de tour revient à effectuer un demi-tour ! Les seules solutions sont a = i et a = – i : tout dépend du sens dans lequel on tourne.
Une autre façon de voir les rotations
En fait, ce petit résultat se généralise assez facilement. Les rotations de centre O et d'angle correspondent exactement aux applications qui, à z, font correspondre
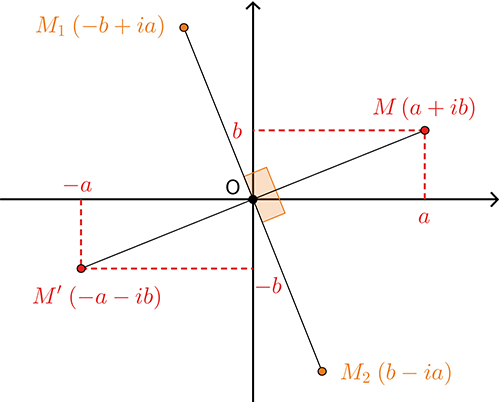
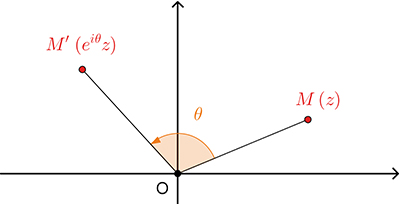
Et si le centre de la rotation n'est pas l'origine du repère ? La situation n'est pas beaucoup plus difficile, il suffit de faire appel aux translations. Comment ces dernières sont-elles décrites dans le cadre des nombres complexes ? Par une addition, ... Lire la suite
