Le théorème de Pick
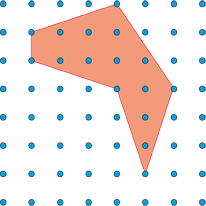Georg Alexander Pick (1859-1942) a découvert une façon étonnante de calculer l'aire de certains polygones, ceux dont les sommets sont sur un maillage orthogonal régulier (constitué des points à coordonnées entières d'un repère orthonormé). Pour mesurer leur aire, Pick compte le nombre i de points du maillage à l'intérieur du polygone ainsi que le nombre b des points du maillage sur le bord du polygone, 10 et 6 dans le cas de la figure. L'aire A est égale à i + b / 2 - 1, ce qui fait 12 ici.
Vérifiez-le !
Pour démontrer la formule de façon générale, on peut commencer par le cas des triangles dont les sommets sont des points du maillage, puis montrer que tout polygone s'obtient en partant d'un triangle de ce type et en en ajoutant progressivement.
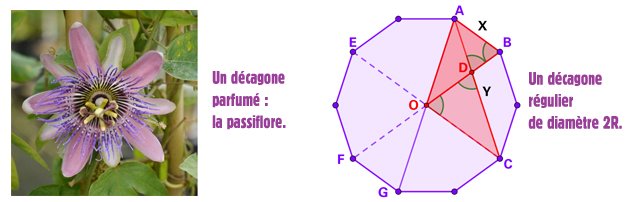
Le décagone sans la trigo
Qui dit polyèdres réguliers dit souvent angles et calculs trigonométriques. Mais pas nécessairement : il est possible de calculer le côté X de ce décagone régulier et celui, Y, du polygone étoilé associé, tous deux inscrits dans un cercle de rayon R, sans un gramme de sinus ou cosinus.
Le théorème de l'angle inscrit s'invite dans ...
Lire la suite gratuitement