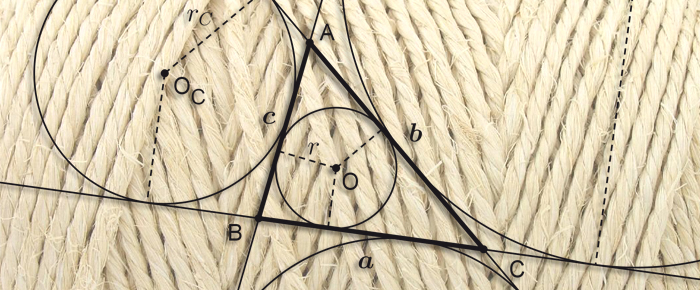
Prenez un bout de ficelle. Chacun en a fait l’expérience, la plus grande surface que l’on puisse délimiter avec une ficelle de longueur donnée est un disque. Qu’en est-il si l’on tend cette ficelle entre trois piquets ? Dit autrement, quel est le triangle de périmètre donné dont l’aire est la plus grande ?
Intuitivement, on peut penser que, pour des raisons de symétrie, c’est le triangle équilatéral qui satisfait à cette condition. Le démontrer semble bien plus difficile. Et pourtant, la formule de Héron permet de s’en sortir à moindres frais !
Et rond, et rond…
Considérons donc un triangle de côtés a, b et c et notons p son demi-périmètre et S son aire. L’inégalité arithmético-géométrique indique que, pour trois nombres positifs x, y et z donnés, on a
avec égalité si, et seulement si, x = y = z.
Appliquons donc cette inégalité à x = p - a, y = p - b et z = p - c.
On a alors x + y + z = 3 p - (a+b+c) = p.
On en déduit que
Il ne reste plus qu’à ajuster les puissances pour obtenir maintenant
