
Au début du XIX e siècle, Jean-Victor Poncelet étudie les polygones inscrits dans une conique, et circonscrits à une autre. En parcourant le périmètre de tels polygones, on effectue une trajectoire fermée dans une courbe fermée, ce qui est un cas particulier des systèmes dynamiques étudiés par les plus grands mathématiciens, d’Henri Poincaré (1854–1912) à Artur Ávila (né en 1979) en passant par Jean-Christophe Yoccoz (1957–2016). Imaginons qu’une boule de billard se déplace sans frottement et obéisse à la loi de réflexion de Descartes lors d’un rebond sur la bande d’un contour fermé. On parle de réflexion spéculaire (semblable à celle de la lumière sur miroir). La question se pose de savoir s’il existe des trajectoires fermées (dont l’origine et l’arrivée coïncident) pour une forme donnée du billard. Mais ce modèle de billard mathématique, donc parfait, a aussi des applications arithmétiques plus ludiques, comme la résolution de problèmes aqueux, pas si sots (voir FOCUS).
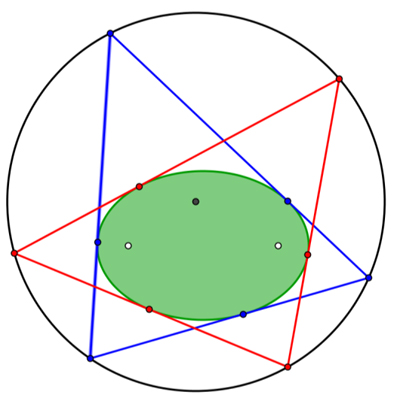
La configuration étudiée par Poncelet.
Des billards de trajectoires
Autre application intéressante, et inattendue, des trajectoires sur un billard : l’arithmétique. On considère un billard rectangulaire de largeur p sur un axe horizontal et de longueur q sur un axe vertical, dans une unité arbitraire, sur ... Lire la suite
