
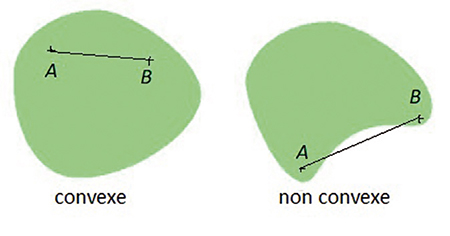
En effet, un sous-ensemble D du plan est convexe si, à chaque fois que l’on choisit deux points A et B quelconques de D, le segment les reliant est, lui aussi, tout entier contenu dans D. Les points du segment sont, en fait, des barycentres à coefficients positifs du système formé par les deux extrémités de ce segment. Par associativité du barycentre, la propriété revient à dire que tout barycentre à coefficients positifs d’un nombre fini de points de D appartient à D.
L’un des problèmes que l’on rencontre dans les applications de la convexité est de déterminer l’enveloppe convexe d’un domaine : elle est définie comme le plus petit convexe contenant le domaine. C’est donc aussi l’intersection de tous les convexes le contenant.
Le théorème de Carathéodory-Steinitz
Même si cela paraît souvent évident graphiquement parlant, l’enveloppe convexe d’un domaine est quelquefois difficile à trouver. En effet, comment trouver tous les convexes le contenant ? D’où l’intérêt du résultat suivant : tout point de l’enveloppe convexe d’un sous-ensemble D du plan est barycentre à coefficients positifs d’au plus trois points de D. Ce théorème, dans le cas où D est borné, date de 1907 et est dû au mathématicien grec Constantin Carathéodory (1873–1950). Il est généralisé en 1914 par le mathématicien allemand Ernst Steinitz (1871–1928) pour tous les sous-ensembles D, bornés ou non.
De plus, selon des raffinements successifs démontrés en 1929 par le mathématicien danois d’origine allemande Moritz Werner Fenchel (1905–1988) puis en 1934 par le Néerlandais Lucas Nicolaas Hendrik Bunt (1905?1984), si D possède au plus deux composantes connexes (« morceaux »), alors tout point de l’enveloppe convexe de D est barycentre à coefficients positifs de deux points de D : pas la peine d’en prendre davantage !
Tous ces résultats se généralisent aux espaces de dimension n (avec n + 1 points en général et n points si le domaine D possède au plus n composantes connexes).
