Les quarante trois auteurs ayant participé au concours de création de problème (on n’avait le droit de proposer qu’un seul problème) ont fait preuve d’une grande inventivité. Les membres du jury ont beaucoup hésité, mais il fallait faire un choix ! C’est souvent en s’appuyant sur la forme et sur la clarté de la solution qu’ils ont trouvé un consensus, mais certains avaient eu un « coup de cœur » pour un problème non retenu. Cet article est l’occasion de mettre en avant quelques-uns d’entre eux. Vous trouverez les solutions, parfois améliorées par les membres du jury, en cliquant sur la question posée.
Pierre-Jean Laurent a choisi « un petit problème de modélisation intéressant, qui demande une interprétation correcte de l’énoncé. Tout est clair aussi bien l’énoncé que la solution, courte mais parfaite. Je le recommande donc ».
Voici donc cet énoncé de Pierre Lemaire.
Promenade sur la plage
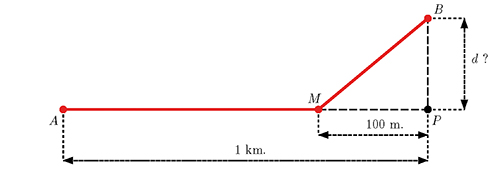
En face du poste de secours, il y a une bouée, prétexte à mon exercice aussi quotidien que régulier. Je pars toujours du point A, situé à exactement 1 km du poste de secours P. Je marche un moment le long de l’eau, toujours à 3 km/h, puis je nage jusqu’à la bouée B, toujours à 2 km/h. J’ai remarqué que c’est lorsque je rentre dans l’eau à 100 m du poste de secours que la durée totale de mon exercice est la plus courte.
À quelle distance du rivage est la bouée ?
Élisabeth Busser a choisi un énoncé d’arithmétique « qui tient en peu de mots, et qu’on peut résoudre sans trop de complications ni de calculs ». Elle a d’ailleurs raccourci la solution d’Arnaud de Ferry, ingénieur retraité passionné de mathématiques, qui a imaginé ce problème en partant des nombres de Kaprekar. En voici l’énoncé.
Quel est mon âge ?
Ma femme a trois ans de plus que moi. Je nous crois encore jeunes ! Pourtant, si j’ajoute le carré de son âge au carré du mien, j’obtiens un nombre à quatre chiffres dont la somme des chiffres est 8.
Philippe Fondanaiche, animateur du site diophante.fr, a choisi « un exercice classique de logique qui demande de mener à bien un raisonnement déductif ». La raison de son choix ? Il considère comme fondamentale cette méthode de résolution et s’inquiète de la voir de plus en plus occultée dans les lycées et collèges. Il s’indigne de voir l’apprentissage des mathématiques limité à l’application « les yeux fermés » de recettes toutes faites ou à l’utilisation de formules sans comprendre leur contenu, une approche qu’il juge de plus en plus en vogue dans l’enseignement.
Voici donc l’énoncé de son coup de cœur, dû à Marie-Pierre Falissard, une des rares femmes à avoir participé au concours de création.
Des amis très particuliers
Mes huit amis logiciens se connaissent bien. Certains mentent tout le temps, les autres jamais. Ils me disent un jour :
Abel : « Je n’aime pas Boole et Frege ment ! »
Boole : « Abel est mon meilleur ami. »
Cantor : « J’ai déménagé et Boole ment ! »
Dedekind : « Tu es mon meilleur ami et Cantor a changé de domicile. »
Erdös : « Dedekind te déteste ! »
Frege : « Erdös ne ment pas. »
Gödel : « Je ne mens pas, mais Frege et Hardy mentent. »
Hardy : « La moitié de tes amis mentent, l’autre moitié non. »
Combien ai-je d’amis, à présent ?
Quant à Raymond Bloch, il a choisi de sélectionner, mais aussi développer (voir encadré) un problème proposé par Thierry Falissard, ingénieur ENPC et passionné d’échecs et de mathématiques. Le problème est, évidemment, lié au placement de pièces d’échecs sur un échiquier. Raymond Bloch : « La recherche de solutions de cette grande famille de problèmes permet des investigations et des découvertes demandant ingénuité, ténacité et rigueur, mais aucune formule mathématique… Elle nous enseigne aussi la prudence nécessaire en face d’une preuve qui semble indestructible, et qui se révèle fausse. J’espère que les lecteurs de Tangente partageront cette énigme avec leurs parents et amis, afin de les convaincre du plaisir que procurent la recherche, et parfois la découverte d’une solution en apparence impossible. Et bravo à l’auteur de cet énoncé. »
Les dames en prise
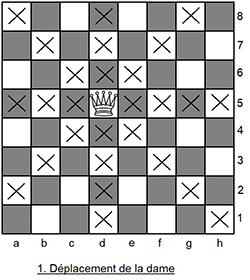
Aux échecs, la dame (D) se déplace verticalement, horizontalement et diagonalement, sur un nombre quelconque de cases (voir figure). Elle peut capturer une pièce adverse située sur une case qu’elle contrôle, en prenant sa place.
Dames en prise
le cas délicieux et surprenant de l’échiquier 7 × 7
Voici deux questions inspirées du dernier problème (de Thierry Falissard), imaginées et résolues par Raymond Bloch.
1. Quel est le maximum possible du nombre total de dames noires et blanches si l’égalité n’est pas exigée entre les nombres de N et de B sur l’échiquier 7 × 7 ?
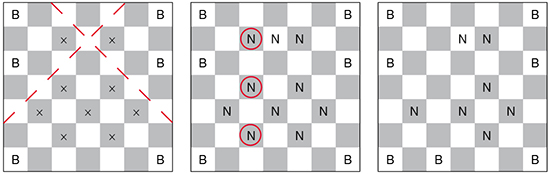
Sur le carré 4 × 4 en bas à gauche, on peut placer huit N sur les huit cases noires, et sur le carré 3 × 3 en haut à droite on peut placer cinq B sur les cinq cases blanches (voir la figure en haut à gauche).
Aucune dame supplémentaire ne peut être ajoutée sur cette configuration, et aucune dame n’attaque une dame de couleur opposée. Donc le nombre maximum de dames possible est 8 + 5 = 13 (*).
Mais Thierry Falissard a produit une solution avec quatorze dames ! Où est l’erreur?
Au lieu d’examiner un carré 4 × 4 et un carré 3 × 3, regardons le carré 5 × 5 en bas à gauche, et le carré 2 × 2 en haut à droite : on peut placer treize B sur les treize cases blanches du carré 5 × 5, et deux N sur les deux cases noires du carré 2 × 2 (voir la figure, au centre : le nombre maximum possible de dames est donc 13 + 2 = 15. Et non pas 13 !
Plus fort encore : dans le carré 6 × 6 en bas à gauche, on peut placer dix-huit dames N sur dix-huit cases noires, et une B dans la case blanche du coin en haut à droite (sur la figure, à droite) : le nombre maximum de dames B et N est finalement 18 + 1 = 19 sur l’échiquier 7 × 7.
2. Thierry Falissard ne demande pas le nombre maximum de dames sur l’échiquier, mais d’y disposer les mêmes nombres de N et de B, en l’occurrence 7 et 7, ne s’attaquant pas mutuellement. Il suffit pour cela d’ajouter une quatorzième dame B à la figure en bas à gauche, et de remplacer une N par une B, mais c’est impossible en vertu de la « preuve » (*).
En fait, cette « preuve » ne démontre que ceci : si l’on place les N sur des cases noires et les B sur des cases blanches, on ne peut pas placer sept B et sept N sur la grille 7 × 7. Il faut donc chercher une configuration différente : l’idée de génie est d’oser placer une N sur une case blanche !
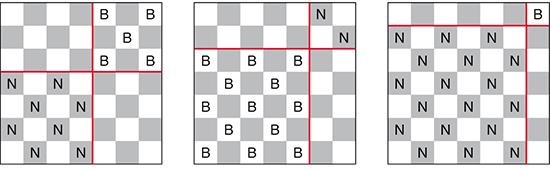
Essayons la stratégie suivante : on place six B sur des cases blanches, puis on marque d’une croix X toutes les cases non attaquées par les six B. Il reste à placer sept N et une B sur les cases X. Si les six B sont placées comme sur la figure suivante (à gauche), il reste deux diagonales blanches totalement libres (en rouge) : on place une N à leur intersection, une décision innovante puisque jusqu’ici les N étaient placées uniquement sur les cases noires. Il y a alors dix cases X disponibles pour les dames N (voir figure suivante, au centre). Il reste à supprimer trois N excédentaires en rouge dans la colonne 3, pour libérer la place d’une septième B en rouge (figure suivante, à droite), qui donne la solution – unique nous dit Thierry Falissard – avec sept B et sept N. R.B.