
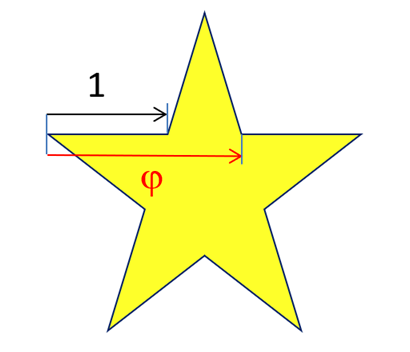
On sait peu de chose des pythagoriciens, sinon que pour eux « tout est nombre (entier) » et que leur symbole était le pentagramme. Ils auraient découvert les nombres irrationnels avec la diagonale du carré, mais d’autres conjecturent que ce serait avec le nombre d’or dans le pentacle. Quoi qu’il en soit, voici une démonstration géométrique de l’irrationalité de φ, rapport entre la diagonale et le côté du pentagone réguliers.
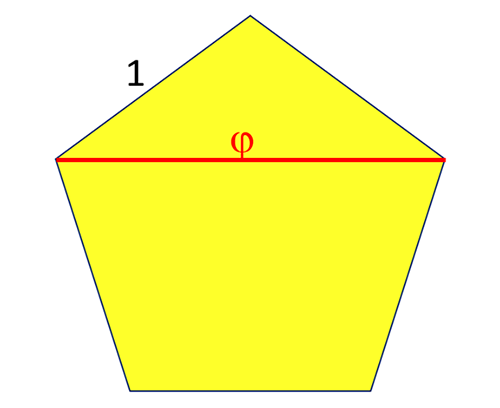
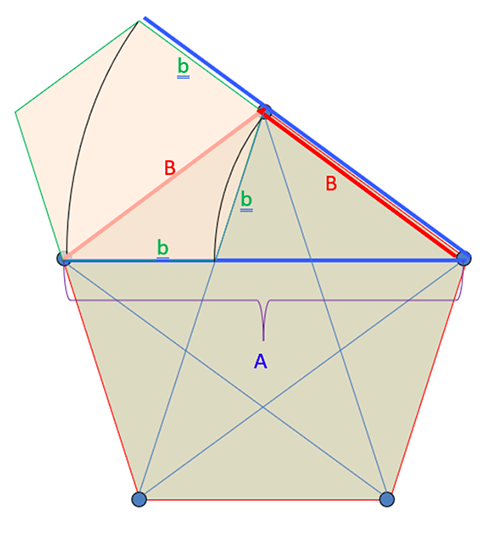
Commençons avec le pentagone rouge. Si φ était un nombre rationnel, on pourrait l’écrire A/B, avec A la diagonale du pentagone rouge et B le côté du pentagone rouge
(A > 0, B > 0, A et B entiers et sans diviseur commun).
Alors b = A − B est un entier, et sur le pentagone construit sur b le nombre d’or, d’après sa définition géométrique, est B/b, avec b < A et A − B < B… ce qui est contraire à l’hypothèse ! Ce raisonnement élémentaire suffit à prouver que φ est irrationnel.
