
Quoi de plus fascinant que les bulles de savon ? Sans aucun doute les films de savon. Une bulle de savon, ça reste une bulle et c’est un petit peu monotone. Certes, on peut en accoler deux, trois ou plus. Mais une bulle, c’est toujours tout rond !
Bulles et films de savon
Les films de savon sont nettement plus variés. On les obtient en trempant des contours en fil de fer ou de cuivre dans une cuve d’eau savonneuse.
Pour faire l’expérience chez vous, utilisez un mélange d’eau, de liquide vaisselle et de glycérine (matière très grasse que l’on trouve en pharmacie et qui permet aux films de savon de tenir plus longtemps). Sinon, vous pouvez aller voir la vidéo de l’auteur « Bulles de savon (expériences) » (14 min, 2021), qui est disponible en ligne sur le site de ressources audiovisuelles pour les mathématiques VideoDiMath.
Lorsque l’on ressort le contour de la cuve, le savon reste accroché à celui-ci et forme une surface dans l’espace. Mais pas n’importe laquelle ! Si l’on répète l’expérience avec divers contours, on observe à la fois une grande variété et une certaine régularité dans ces formes que prend le savon. Que peut-on en dire ? N’hésitez pas à réaliser vous-même des expériences chez vous avant toute chose !
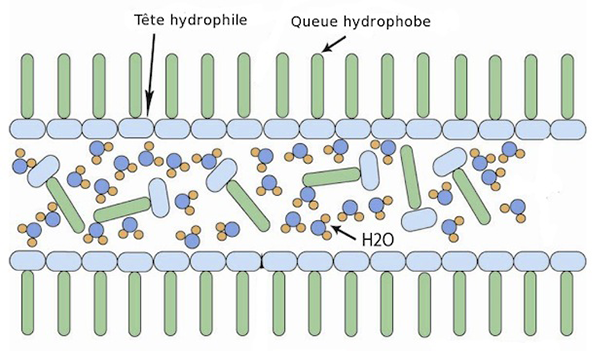
Un film de savon est composé d’une couche d’eau entourée de deux couches de molécules savonneuses (pour une épaisseur totale de l’ordre du micron). Ces dernières ont une tête hydrophile et une queue hydrophobe, ce qui les amène à se positionner comme sur le dessin, la tête hydrophile vers l’intérieur (vers la couche d’eau) et la queue hydrophobe vers l’extérieur (l’air). Les deux couches extérieures de savon retardent l’évaporation en évitant le contact de l’eau avec l’air. C’est pourquoi une bulle de savon n’éclate pas tout de suite.
L’énergie potentielle d’un film de savon est proportionnelle à son aire. À l’équilibre (en négligeant toutefois les effets de la gravité, ou du vent…), le savon va donc minimiser l’aire du film qu’il forme. Enfin, il va la minimiser localement : cela signifie que, si l’on perturbe la surface « un petit peu », son aire va augmenter. Par contre, il n’est pas certain que le savon aille chercher la surface d’aire la plus petite possible ; les minima locaux de l’aire sont stables. Il faut penser à un ballon dans un paysage vallonné. Celui-ci sera en équilibre dans un creux, mais ce n’est pas forcément le point d’altitude minimale du paysage.

Le caténoïde étant matérialisé par un film de savon,
il s'agit d'une surface minimale.
Minimiser l’aire sous contraintes
Si le savon prend ces formes magnifiques, régulières mais parfois surprenantes, c’est tout simplement parce qu’il cherche la surface qui a la plus petite aire possible sous les contraintes qu’on lui impose. Dans les bulles de savon, on lui impose d’enclore un volume d’air fixé : il prend donc la forme qui minimise l’aire et qui enferme un volume fixé.

Dans le cas de plusieurs bulles, le savon va trouver la forme qui minimise l’aire totale tout en enfermant plusieurs volumes distincts et séparés (qui peuvent être égaux ou différents). Pour les films de savon, la contrainte est de s’accrocher au contour (l’énergie nécessaire pour se détacher étant trop importante). On peut aussi imaginer mélanger les contraintes.
Et nous voilà arrivés, sans même nous en rendre compte, dans le domaine des mathématiques. Nous avons ramené la compréhension des formes des films de savon à une question géométrique bien posée : quelles sont les propriétés des surfaces d’aire minimale sous certaines contraintes ?
Avant de se lancer pour les surfaces dans l’espace, il est toujours intéressant, geste mathématique essentiel, de simplifier le problème. Regardons d’abord ce qu’il se passe pour des courbes dans le plan. Essayons de minimiser la longueur totale d’une courbe plane qui doit relier des points entre eux. C’est le problème des autoroutes. Étant donnés quelques points dans le plan (des villages), trouver une courbe (un réseau routier) qui relie tous ces points les uns aux autres et qui est de longueur totale minimale. On peut même le faire avec du savon en imposant une symétrie par translation verticale !
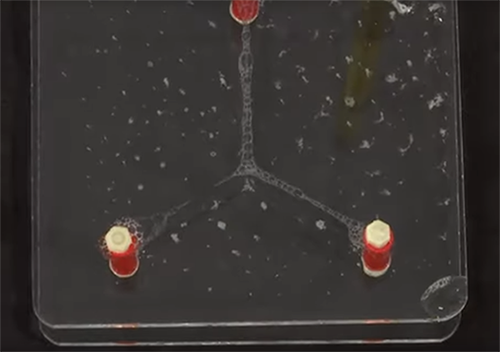

La solution fournie par l’eau savonneuse pour trois villes et quatre villes.
Déjà, les routes seront droites, c’est-à-dire que la courbe sera composée de segments de droites (car en géométrie euclidienne la droite est le chemin le plus court joignant deux points). Mais ces segments peuvent s’intersecter. À chaque intersection arrivent trois routes et elles forment des angles de 120 degrés (voir par exemple la vidéo de l’auteur « Bulles de savon (explications) » (19 min, 2021), elle aussi disponible sur VideoDiMath).
En général, la configuration optimale n’est pas simple à obtenir mais des algorithmes pour la trouver existent. Ils reposent sur la preuve qu’il existe un nombre fini de configurations possibles (c’est-à-dire des segments partant des points de départ avec des intersections trois par trois à angles égaux) qu’il n’y a qu’à tester une par une. Mais ça peut être long ! Une autre solution consiste à tremper une plaque avec des plots dans le savon ; cela nous donnera la solution.
Mais dans l’espace, qu’est-ce qui remplace les droites ? Les surfaces qui minimisent l’aire sont appelées des surfaces minimales. Elles ont une courbure moyenne nulle.
Prenons une surface S et un point sur S. Le plan tangent est le plan qui « approche » le mieux la surface au voisinage de ce point. Dans le cas d’une sphère par exemple, c’est tout simplement le plan qui vient se poser sur la sphère en ce point. Une direction orthogonale à ce plan tangent est appelée la normale à la surface en ce point (il y a deux choix, mais on peut en fixer une).
Imaginons maintenant un plan contenant cette direction normale, donc un plan orthogonal au plan tangent. Son intersection avec la surface est une courbe plane. Cette courbe possède une courbure. On lui donne un signe en disant qu’elle est positive si la courbe tourne vers la normale choisie (et négative sinon). On obtient ainsi une collection de courbures correspondant à toutes les intersections de la surface avec des plans orthogonaux au plan tangent. Un résultat de Leonhard Euler (1707‒1783) stipule que ces courbures atteignent un maximum et un minimum dans deux directions orthogonales. Ce sont les deux directions de courbure principale qui donnent deux courbures. La moyenne de ces deux courbures est… la courbure moyenne. Dire que ce nombre est nul revient à dire que, localement, on est toujours dans la configuration de la selle de cheval, avec les deux courbures égales au signe près.

Il y a donc deux grands modèles locaux de surface minimale : le plan et la selle de cheval avec courbures égales. Ce monde est tout de même beaucoup plus vaste que celui des droites dans le plan, puisque ces modèles locaux peuvent donner lieu à une grande variété de surfaces.
De Joseph Plateau à Jean Taylor
Au XIX e siècle, un physicien et mathématicien belge, Joseph Antoine Ferdinand Plateau (1801‒1883), a également été fasciné par les films de savon, au point d’écrire un traité volumineux en grande partie consacré à ce sujet : Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires (1873). Quand Plateau écrit ce livre, il est aveugle. Mais il a fait ces observations avant de le devenir et il a des assistants compétents pour refaire les expériences. Il décrit très précisément comment conduire ces expériences, comment compenser les effets de la gravitation, comment mesurer les angles très finement.
Au terme de ces observations, il en arrive à exprimer trois lois auxquelles obéissent les films de savon :
• Ils sont constitués de surfaces régulières qui sont minimales (c’est exactement ce que l’on vient de voir ; à la régularité près, ce phénomène est déjà connu à l’époque) ;
• Ces surfaces s’intersectent trois par trois le long d’arêtes en formant des angles de 120 degrés ;
• Ces arêtes s’intersectent quatre par quatre en formant l’angle au centre du tétraèdre régulier (cet angle, d’une valeur approximative de 109,47°, est celui dont le cosinus vaut et dont le sinus vaut
).
Ces lois, que Plateau ne démontre pas, deviennent une conjecture qui tiendra un siècle. En 1976, la mathématicienne américaine Jean Taylor (née en 1944), publie dans la prestigieuse revue Annals of Mathematics une preuve de ces lois. Et ceci prouve que, contre toutes les apparences, ceci n’est pas un carré :

En effet, si cela en était un, il y aurait des angles de 90 degrés. Or, les angles d’intersection des arêtes doivent être supérieurs à 109°.
Mais si la petite figure centrale n’est pas un carré, par symétrie, les côtés de cette figure ne peuvent être rectilignes. Ce qui signifie que les surfaces qui s’accrochent au bord, contre toute apparence également, ne sont pas planaires. Ce sont des surfaces minimales mais ce ne sont pas des plans qui, eux, s’intersecteraient nécessairement le long de segments de droites.
Comme quoi, les films de savon peuvent être surprenants ! Ils n’ont d’ailleurs pas encore livré tous leurs secrets mathématiques, loin s’en faut…

Contrairement à ce que l'on pourrait penser,
en plongeant une structure cubique dans une solution savonneuse,
on n’obtient pas un « modèle réduit » du cube.
Le résultat a approximativement la forme d’un carré entouré
de surfaces non planes.
Ce texte est issu de la conférence « De Joseph Plateau à Jean Taylor, des bulles de savon bien inspirantes » donnée par l’auteur le mercredi 23 mars 2022 dans le cadre du cycle « Un texte, un mathématicien » à la Bibliothèque nationale de France. Olivier Druet est directeur de recherche au CNRS à l’Institut Camille-Jordan, université Lyon-I. Il est aussi directeur de la Maison des mathématiques et de l’informatique (MMI) de Lyon.
