
La conjecture de Singmaster
Pour n et p entiers naturels avec p ≤ n, le coefficient binomial est le nombre de manières de choisir p objets parmi n, sans tenir compte de l’ordre.
Il est égal à
où n! désigne la factorielle de n, soit le produit de tous les nombres entiers de 1 à n.
Le nombre est, par définition, un entier.
Prenez le début du triangle de Pascal, formé des coefficients binomiaux
où n est donné sur les lignes et p sur les colonnes :
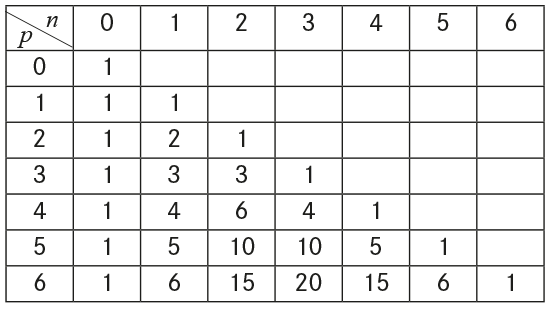
L’entier 1 est présent plusieurs fois. Il est facile de comprendre qu’il va apparaître en fait une infinité de fois puisqu’il appartient à toutes les lignes. Mais c’est le seul car tout entier C tel que C > 1 ne peut apparaître que dans les C+1 premières lignes du triangle.
L’entier 6 est présent trois fois : une fois pour n = 4 et deux fois pour n = 6. Il ne peut plus apparaître ensuite. Si l’on note N(t) le nombre d’apparitions de l’entier t, on a ... Lire la suite gratuitement
