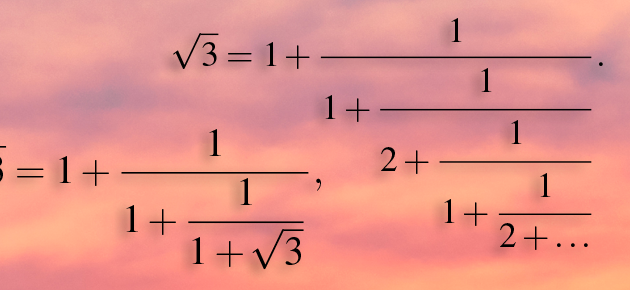
Dans l’histoire des mathématiques, la notation décimale est relativement récente : sans doute introduite par les mathématiciens arabes, elle est vulgarisée de manière indépendante par le Flamand Simon Stevin (1548‒1620). Elle est très vite devenue incontournable. À l’heure actuelle, avec l’utilisation des calculateurs numériques, que ferait-on sans cette écriture ?
Avant la notation décimale
Auparavant, l’écriture fractionnaire était utilisée. Ainsi, chez les Égyptiens, le nombre 2,75 s’écrivait (avec les notations actuelles) 2 + 1/2 + 1/4. Ce type d’écriture perdura jusqu’au XVIe siècle. Mais comment faire pour représenter des nombres irrationnels, qui, par définition, ne possèdent pas d’écriture fractionnaire ? C’est là qu’interviennent les fractions continues !
La notation en fraction continue est liée à l’algorithme d’Euclide.
Il s’agit de représenter un nombre x sous la forme
avec α, β, γ… entiers, c’est-à-dire en utilisant uniquement des fractions dont le numérateur vaut 1.
Par exemple, on peut écrire 47/6 de la manière suivante :
Ainsi, quand le reste de la division euclidienne vaut 1, l’algorithme s’arrête. Cela se produit pour toutes les fractions. Par contre, lorsque qu’un nombre n’est pas rationnel, son développement ... Lire la suite
