
La notion de tangence est celle de la linéarisation locale d’une courbe. Le cercle, pouvant être considéré comme la plus simple et esthétique courbe, apparaît naturellement dans de nombreux problèmes de tangence. Au IIIe siècle avant notre ère, Archimède traite ainsi, entre autres, de l’arbelos (voir article « L'arbelos d'Archimède à Pappus ») et Apollonius de Perge de problèmes de contacts entre cercles, droites et points. On n’a gardé trace du Traité des contacts d’Apollonius que grâce à Pappus d’Alexandrie, qui fut l’un des principaux propagateurs de la culture mathématique grecque. Les résumés partiels qu’il fit des œuvres perdues de l’Antiquité suscitèrent la curiosité de nombreux mathématiciens des XVIe et XVIIe siècles, comme François Viète (1540‒1603) et René Descartes (1596‒1650).
Vers l’inversion
À la fin du XVe siècle, Regiomontanus (1436‒1476) avait trouvé une solution algébrique au dixième et dernier problème d’Apollonius, « trouver un cercle tangent à trois cercles donnés ».
François Viète mit alors au défi le médecin et mathématicien d’outre-Quiévrain Adrien Romain (1561‒1615) de résoudre géométriquement ce problème. Ce dernier en donne rapidement une solution, mais à l’aide de coniques, ce qui ne peut satisfaire un puriste : « Éminent Adrien, tant qu’on touche le cercle par des hyperboles, on ne le touche pas finement. »
François Viète reconstitue alors les solutions perdues du Traité des contacts dans son Apollonius Gallus. À sa suite, Descartes complète ce problème en 1643 par un théorème (voir encadré), que Fermat généralisera avec des sphères.
Si Viète se restreint, par esthétisme classique, aux résolutions à la règle et au compas, les mathématiciens du XIX e siècle Michel Chasles (1793‒1880) et Joseph Louis François Bertrand (1822‒1900) trouveront néanmoins, dans sa remarquable nouvelle algèbre, traces d’éléments précurseurs aux inventions du triangle sphérique et de l’inversion plane (voir encadré). Précisément, illustrons avec l’inversion la construction de problèmes de cercles tangents, de façon bien plus « lisible » qu’à la règle et au compas.
L’inversion
Une inversion i de pôle O est, comme les symétries, une transformation involutive, donc telle que Elle fait correspondre à tout point A différent du pôle O le point image, ou homologue, A’ = i(A) sur la droite (OA) tel que
Le cercle (C) de centre O et de rayon OP = R, appelé cercle d’inversion, est la frontière entre les points intérieurs et extérieurs échangés par l’inversion et est donc invariant point par point.
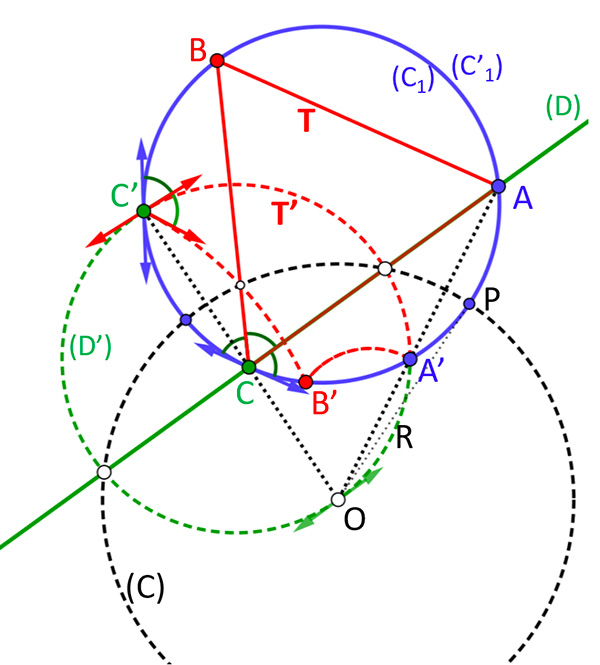
L’inverse d’un cercle qui ne passe pas par le pôle est un cercle, sinon on obtient une droite (D) parallèle à la tangente au cercle (D’) au pôle O. Réciproquement, l’inverse d’une droite est un cercle passant par le pôle. L’ensemble des cercles du plan (les droites étant des cercles « de rayon infini ») est donc stable par inversion. Le cercle (C1) est quant à lui globalement invariant puisque la puissance du pôle O par rapport à (C1) est OP2 = R2. La partie extérieure à (C) est en correspondance point par point avec la partie intérieure.
L’un des grands intérêts de l’inversion comme « outil géométrique » est d’être une transformation conforme : elle conserve les angles, à défaut des distances. Sur la figure, le triangle équilatéral T a ainsi pour image le triangle curviligne T’, dont les angles au sommet sont aussi de 60°.
Le grand intérêt de l’inversion est d’être une transformation involutive (égale à sa propre inverse) et conforme (conservant les angles, et donc les tangences entre courbes). La stratégie de construction d’une solution est alors d’effectuer une inversion qui simplifie le problème, de le résoudre, puis de « revenir » par la même inversion à la configuration initiale.
Construisons trois demi-cercles à partir des trois points alignés A, B et C. La forme obtenue est, depuis Archimède, associée à un tranchet de savetier, ou arbelos (voir article « L'arbelos d'Archimède à Pappus »). Intéressons-nous aux cercles tangents à l’arbelos (de rayons r et ρ) et à la tangente (BD) commune aux cercles internes (C1) et (C2). En abordant le problème de façon « traditionnelle », on a, par construction,
r3 = r1 + r2 et, avec les deux triangles rectangles O1ω1H et O3ω1H,
c’est-à-dire (r1 + r)2‒ (r1 ‒ r)2 = (r1 + r2 ‒ r)2 ‒ (r2 ‒ r1 + r)2 car O3H = CH – r3.
On obtient alors
Cette expression, symétrique en r1 et r2, nous permet de conclure que ρ = r. Les deux cercles ont le même rayon : ce sont les cercles jumeaux d’Archimède.
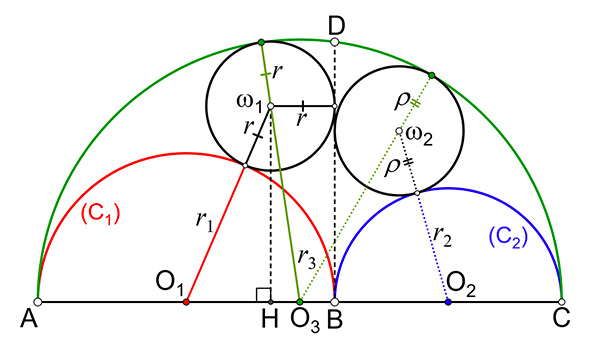
Les cercles jumeaux d’Archimède.
Une autre façon de faire, en intime relation avec les problèmes de cercles tangents, est d’utiliser l’inversion. Trouver les cercles tangents à deux droites parallèles ne pose pas de problème. Il semble donc naturel d’essayer une inversion dont le pôle est le point de contact de deux cercles, comme les points A, B et C.
Prenons pour cercle d’inversion (et donc comme ensemble des points invariants) le cercle (C) de centre, ou pôle, le point A de contact des cercles (C1) et (C3), eux-mêmes tangents au cercle (γ1), et de rayon tel que le cercle (γ1) soit invariant.
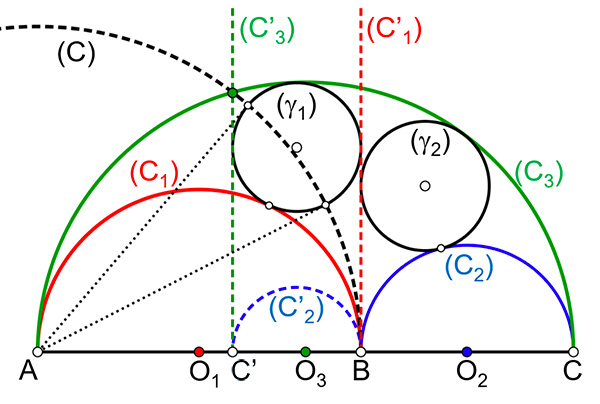
Inversion des cercles jumeaux avec le pôle en A.
Cette inversion transforme les cercles (C1) et (C3) en les droites (C’1) et (C’3). Tous les cercles initialement tangents à ces deux cercles (C1) et (C3) auront alors pour inverses des cercles de même diamètre, correspondant à l’écartement entre les deux droites (C’1) et (C’3). Il en est ainsi pour les cercles (γ1) et (C’2).
Le point C’ étant l’inverse du point C, on a, par définition de l’inversion : AC’×AC = AB2, ce qui donne
On retrouve, heureusement, le fait que et que, par pure symétrie, les cercles (γ1) et (γ’1) ont le même rayon. Avec le même argument de symétrie, on aurait pu arriver au même résultat en considérant pour cercle d’inversion celui de centre C laissant (γ’1) globalement invariant.
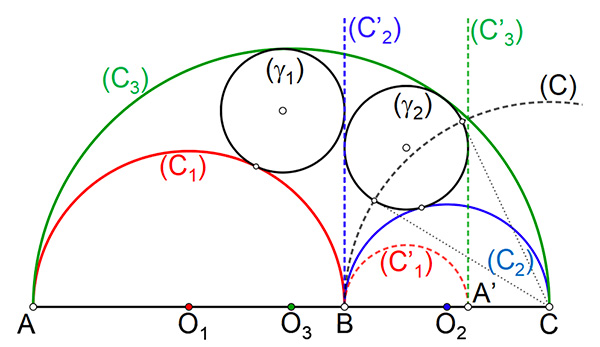
Inversion des cercles jumeaux avec le pôle en C.
Des cercles à la chaîne
La « corne » de l’arbelos délimitée par les cercles (C1 ) et (C3 ) de la figure qui suit peut être remplie d’une « infinité » de cercles tangents pour constituer la chaîne de Pappus. En s’inspirant de l’étude précédente, effectuons l’inversion de pôle A et de cercle d’inversion (C) qui laisse invariant un cercle quelconque de la chaîne, ici ( Γ3).
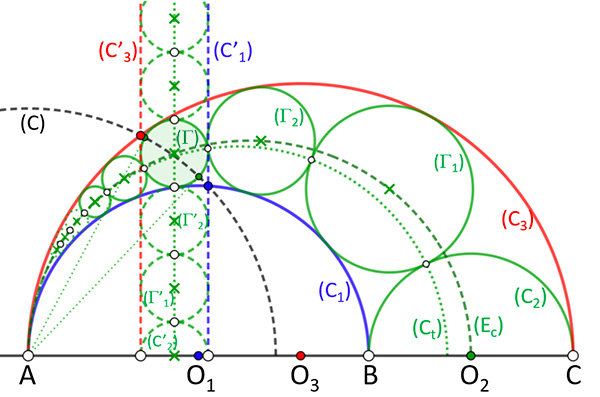
La chaîne de Pappus.
Comme précédemment, les images des deux cercles frontières (C1 ) et (C3 ) seront les droites (C’1 ) et (C’3 ), ce qui implique naturellement que tous les cercles images (Γ’n ) des cercles (Γn ) de la chaîne par l’inversion seront tangents à ces deux droites et auront donc le même diamètre ϕn . On en déduit que l’altitude zn du centre du nème cercle (Γn ) par rapport aux diamètres des cercles frontières est proportionnelle à son diamètre ϕn : zn = nϕn .
Cette figure permet aussi d’illustrer les propriétés caractéristiques de l’inversion, la conservation des angles et non des distances. Ainsi, si les centres et les points de contact des cercles (Γ’n ) sont bien alignés, leurs images par l’inversion de cercle (C) sont sur deux courbes différentes. Les points de contact sont conservés par l’inversion et, l’image d’une droite étant un cercle, sont cocycliques sur le cercle (Ct ). Par contre, la notion de centre étant une notion métrique, les centres des cercles (Γn ) et (Γ’n ) ne se correspondent pas. L’ensemble des centres des cercles de la chaîne de Pappus est sur l’ellipse (Ec ) de foyers O1 et O3 et de grand axe [AO2 ], comme démontré dans un cas général ci-après.
La version de Steiner
Un problème similaire porte le nom de l’inventeur de l’inversion, la chaîne de Steiner, version finie de celle de Pappus. Il s’agit d’une suite finie de cercles, chacun tangent à son prédécesseur et à son successeur, et de plus tangents à deux cercles donnés. Dans le cas classique présenté ici, ces cercles initiaux n’ont en commun que des points intérieurs, c’est-à-dire que l’un contient strictement l’autre. Cette construction contient une vérité géométrique intrinsèque que l’on appelle porismede Steiner : « s’il existe une chaîne fermée de n cercles (Cn ) (donc tels que (Cn ) = (C1 )), alors il en existe une infinité. »
On utilise la propriété de l’inversion de pouvoir transformer deux cercles en deux droites, si les cercles se coupent, ou en deux cercles concentriques sinon. On part donc de deux cercles concentriques (Γ1) et (Γ2), et on remplit l’espace interne de cercles tangents, nécessairement de même rayon. Cette construction n’est possible que pour certaines conditions entre les rayons des cercles initiaux.
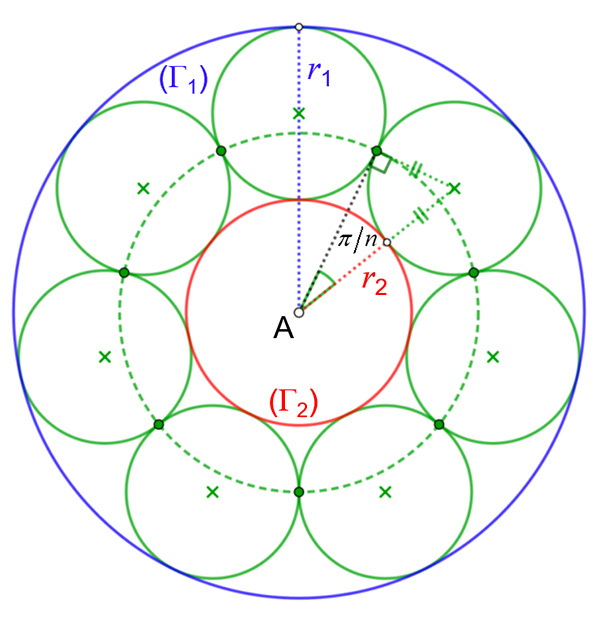
Configuration initiale de la chaîne de Steiner.
Un calcul rapide montre que l’on doit avoir :
On effectue alors une inversion de cercle (C) qui conserve le cercle extérieur (Γ1 ) et transforme le cercle (Γ2 ) à la dimension souhaitée en choisissant correctement le pôle O. Puisque, dans la figure initiale, les cercles concentriques sont stables par le groupe des rotations autour de leur centre, le nombre de configurations possibles a la puissance du continu et est donc infini.
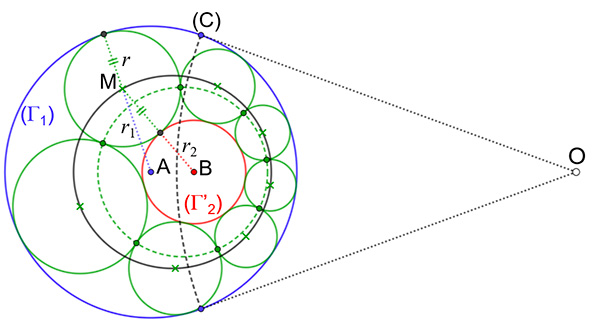
La chaîne de Steiner après inversion de cercle (C).
Sur cette dernière figure, on montre que pour tout centre M d’un cercle interne de la configuration finale, on a AM + BM = r1 + r2, qui est l’équation d’une ellipse admettant les centres des cercles initiaux pour foyers. Cette démonstration est bien sûr encore valide dans le cas limite de la chaîne de Pappus, lorsque les cercles (Γ1) et (Γ2) deviennent tangents.
Grâce à l’inversion, on vient de découvrir que là où il y a de la « chaîne », il peut y avoir du plaisir ! Sachez aussi que cette transformation, utile pour ces problèmes « engeance de tangence », peut être judicieusement utilisée pour résoudre certains sangaku « sans à-coups ».
Le théorème de Descartes
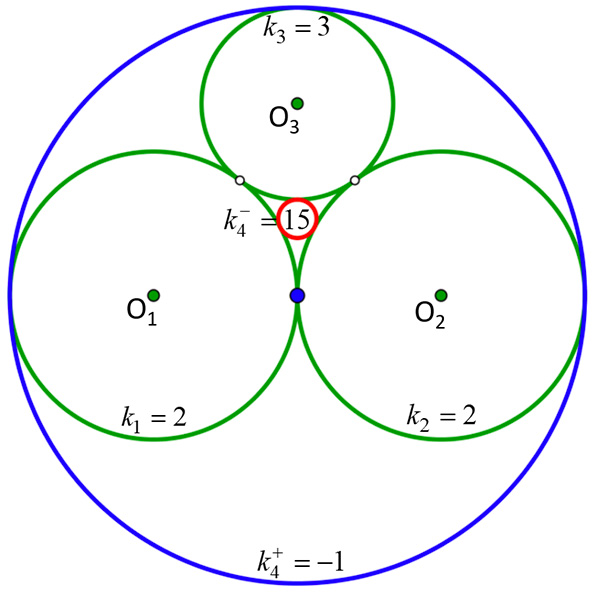
Le théorème de Descartes exprime une relation entre les courbures de quatre cercles tangents deux à deux. La courbure d’un cercle est l’inverse de son rayon. En donnant aux courbures le même signe pour deux cercles extérieurs et un signe contraire sinon, on a la relation
Cette équation du second degré a alors deux solutions, et
,données par
et
courbures de cercles appelés, de façon inappropriée, cercles de Soddy.
On en déduit que la somme des courbures solutions est
Si les trois cercles initiaux ont une courbure entière et que k1k2 + k2k3 + k3k1 est un carré, alors les courbures et
sont entières et de même parité.
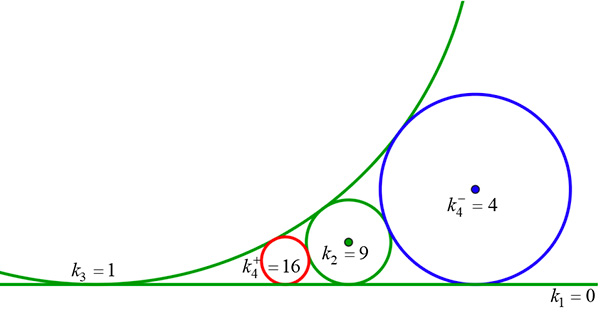
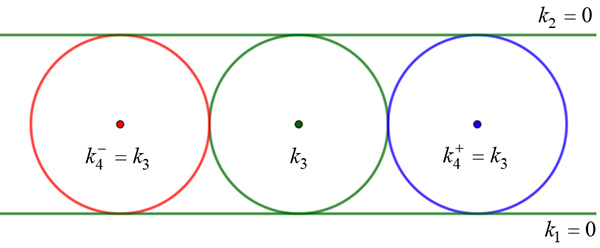
Une droite pouvant être considérée comme un cercle de courbure nulle, par exemple k3 = 0, il existe encore dans ce cas deux solutions et
, données par
et
Et même avec deux droites (k1 = k2 = 0), la relation tient encore ! Les droites devant être tangentes, cela veut dire qu’elles sont parallèles tout en étant tangentes au cercle de rayon Il y a donc encore deux solutions telles que
et
références
• Dossier « Puissance d’un point ». Tangente 208, 2022. • Le cercle. Bibliothèque Tangente 36, 2009. • Géométrie. Marcel Berger, Nathan, 2000.


