Le problème de Didon

C’est par quelques vers du livre premier de l’Énéide de Virgile que le « problème de Didon » est arrivé à la notoriété. Énée, prince troyen, apprend de la bouche de Vénus comment la princesse phénicienne Elyssa (Didon), après avoir fui depuis Tyr (aujourd’hui au Liban) la tyrannie de son frère meurtrier, arriva sur la côte de l’actuelle Tunisie pour s’y établir.

Une ruse historique

Il faut le commentaire du grammairien Servius (fin du IV^e siècle) pour comprendre la ruse de Didon : « Échouée en Libye, Didon se vit d’abord chassée par Hiarbas ; ensuite, elle demanda, par ruse (callide), d’acheter autant de terre qu’une peau de bœuf pouvait en tenir (tenere). » C’est sur ce double sens du verbe tenere que repose la ruse de Didon. Hiarbas, le roi local, comprend qu’il cédera un territoire recouvert par une peau de bœuf, donc ridiculement petit ; Didon entend récupérer un territoire entouré par une peau de bœuf (ce sur quoi insiste Virgile par l’emploi de circumdare au lieu de tenere) et qu’il suffit de découper cette peau en fines lanières que l’on coudra bout à bout et qui entoureront un territoire bien plus vaste.

Cette ruse (le découpage de la peau) se retrouve dans de nombreuses légendes, des Hottentots d’Afrique australe aux Kirghizes d’Asie centrale, jusqu’à l’Histoire des Rois de Bretagne (XII^e siècle). Mais ce qui nous intéresse ici, c’est comment entourer la plus grande surface possible avec une courbe de longueur donnée, donc avec un même périmètre (d’où « isopérimétrique »), problème dont Didon semblait connaître (au moins intuitivement) la réponse puisque le site archéologique de Carthage nous montre que la forteresse initiale avait la forme d’un demi-cercle adossé à la mer. En effet, la courbe qui entoure la surface maximale pour un périmètre donné est le cercle (ou le demi-cercle pour une courbe adossée à une droite).

Le mystérieux Zénodore

Qu’en était-il, dans l’Antiquité, de la réponse à cette énigme ? Aristote (‒384 ; ‒322), dans son traité De caelo (« Du ciel »), indique, pour la trajectoire des astres : « Le chemin le plus court pour que ces objets retournent à leur point de départ est représenté par la circonférence d’un cercle. » Peut-être connaissait-il la réponse au problème de Didon ? Il en est peut-être de même d’Archimède (‒287 ; ‒212)… Le philosophe néoplatonicien Simplicius, dans son commentaire sur De caelo au VI^e siècle, le crédite en effet d’une solution, mais cela est contesté. La première approche mathématique avérée est à mettre au crédit du mathématicien grec Zénodore, qui vécut entre le troisième siècle avant notre ère et le premier siècle de notre ère, probablement peu de temps après Archimède. Son traité, Sur les figures isopérimétriques, qui a été malheureusement perdu, est connu par les commentaires qu’en ont fait au IV^e siècle Théon d’Alexandrie dans sa recension de La Syntaxe mathématique de Ptolémée (aujourd’hui appelée l’Almageste) et Pappus dans sa Collection mathématique.

Zénodore aurait ainsi prouvé deux résultats :

l’aire d’un polygone régulier de n côtés est supérieure à l’aire de tout autre polygone de n côtés ;

si l’on considère deux polygones réguliers, l’un de n₁ côtés, l’autre de n₂ côtés, avec n₂ > n₁, alors le polygone à n₂ côtés délimite une surface plus grande.

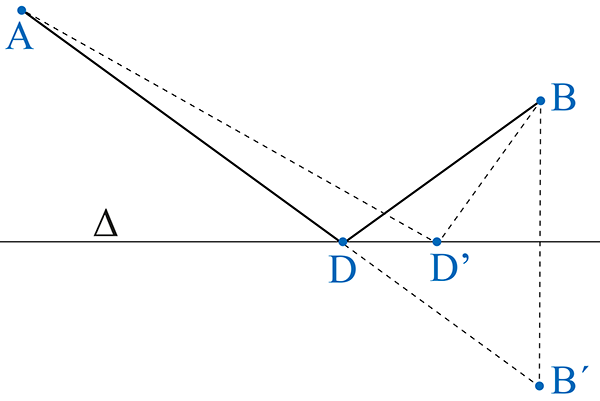
Pour établir ces propositions, Zénodore s’appuie sur un résultat très connu depuis Héron d’Alexandrie (I^er siècle) pour résoudre le problème suivant : si deux points A et B sont du même côté d’une droite Δ, comment trouver le point D sur la droite Δ tel que la somme des distances de A à D et de D à B soit minimale ? En fait, on obtient ce point en traçant le symétrique B’ de B par rapport à la droite Δ et en traçant une droite reliant A à B’. La ligne droite étant le plus court chemin entre deux points, AD + DB’ < AD’ +D’B’, et donc le plus court chemin recherché est AD + DB.

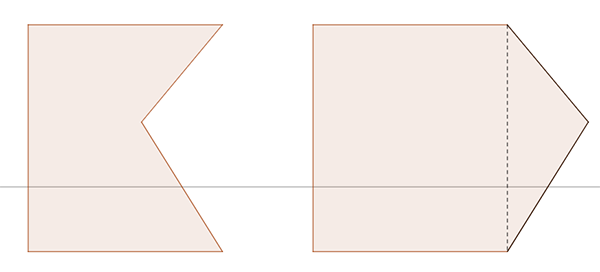
Par ailleurs il était déjà bien connu que, à périmètre constant, le polygone d’aire maximale ne pouvait être que convexe puisque si l’on construit le symétrique de la partie non convexe par rapport au segment la délimitant, on obtient de façon évidente une courbe de même périmètre entourant une surface plus grande.

Le miel des abeilles

L’apport de Pappus au problème isopérimétrique est double. Dans son livre V intitulé Sur la sagacité des abeilles, il explique la structure hexagonale des rayons de cire où les abeilles stockent leur miel. Il s’agit de paver une surface plane avec des structures régulières ne présentant aucun interstice ; on parle d’un pavage total du plan. Or, cela n’est possible qu’avec trois types de polygones réguliers : des triangles équilatéraux, des carrés et des hexagones. Donc, d’après les résultats de Zénodore, la structure permettant de stocker le maximum de miel est celle qui présente le plus de côtés : l’hexagone !

Mais Pappus montre aussi, apport déterminant au problème isopérimétrique, que parmi tous les segments circulaires ayant la même circonférence, celui qui a la plus grande surface est le demi-cercle.

Une démonstration plus récente et d’une grande ingéniosité, mais toujours par de purs procédés géométriques, est due au mathématicien suisse Jakob Steiner. Pour ce faire, il s’appuie d’abord sur deux propriétés des triangles :

• tout triangle inscrit dans un cercle, dont un côté est un diamètre du cercle, est un triangle rectangle ; le diamètre en est alors l’hypoténuse ;

• de tous les triangles dont deux côtés ont des longueurs données, le triangle de plus grande surface est le triangle rectangle dont les deux côtés donnés sont les côtés perpendiculaires.

Ensuite, il prend deux points A et B sur une droite Δ et il suppose que la courbe maximisant l’aire entre cette courbe et le segment [AB] n’est pas un demi-cercle.

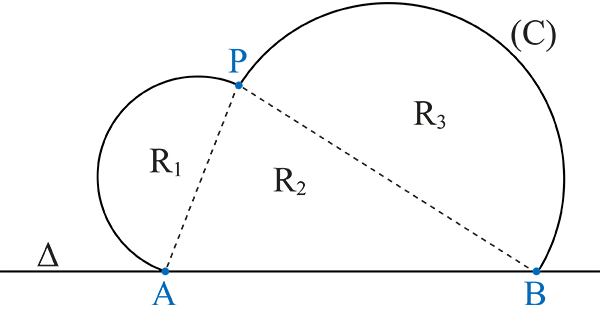
On a donc un point P tel que l’angle  est différent de 90°. Maintenant, on suppose que les cordes AP (arc de cercle) et PB (arc de cercle) sont « rigides » et l’on fait « coulisser » A et/ou B en A’ ou B’ de façon à avoir un angle droit pour 

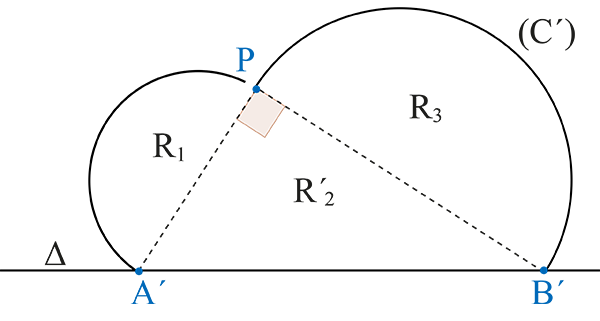
D’après la seconde propriété des triangles citée plus haut, l’aire R’₂ est supérieure à l’aire R₂ et on a donc une courbe (C) qui peut se transformer en une courbe (C’) de même périmètre et qui entoure (avec la droite Δ) une aire supérieure à celle entourée par (C) et Δ. La seule courbe (C) qui ne permettrait pas cet accroissement de surface serait donc un demi-cercle (puisqu’on n’y trouverait pas de point P tel que l’angle  soit différent de 90°).

Ces approches géométriques, antiques ou modernes, tout en élégance et en ingéniosité, évitent cependant des questions importantes. Ces courbes maximales doivent posséder certaines propriétés… si elles existent ! Mais existent-elles, ces courbes ? On trouve de multiples problèmes géométriques de cet ordre qui n’ont pas de solution : ainsi, il est impossible de trouver une figure convexe d’aire maximale parmi toutes les figures convexes qui ont un périmètre inférieur à 1 ; de même, le problème de Kakeya, qui demande quelle est la surface d’aire minimale dans laquelle une aiguille de longueur donnée peut effectuer une rotation de 360°, n’admet lui non plus pas de solution.

L’approche analytique

C’est une approche analytique qui va permettre de surmonter cette difficulté. Les premiers éléments de réponse sont fournis par le mathématicien suisse Jacques Bernoulli (1654‒1705), qui utilise de nouveaux outils issus du calcul différentiel. Dans la continuité de cette démarche apparaît une nouvelle hypothèse : la frontière du domaine doit être « lisse », c’est-à-dire qu’elle admette une tangente en tout point. Cela se traduit par la propriété que les fonctions la définissant doivent être « suffisamment différentiables ». Une ondulation sur la frontière a tendance à augmenter davantage le périmètre plutôt que l’aire et plus cette courbe frontière est irrégulière, plus elle s’écarte de l’optimale. C’est au mathématicien allemand Karl Weierstrass (1815‒1897) qu’il revient de formaliser le calcul des variations. Il étudie non plus une courbe spécifique, mais un ensemble de courbes qui ne diffèrent que d’un paramètre. En faisant varier ce paramètre, il montre que le cercle est la courbe optimale recherchée.

Les notions de longueur d’une courbe et de surface entourée par une courbe ont été par ailleurs précisées par le Français Camille Jordan (1838‒1922). Or, toute courbe fermée continue peut être approchée par des courbes « lisses ». Ainsi l’approche fondée sur le calcul variationnel aboutit-elle au moins en dimension 2 (en général, on a l’inégalité
p ² ≥ 4 π a où a désigne l’aire intérieure à la courbe de périmètre p). En dimension 3, une démonstration que la solution est la sphère est obtenue en 1884 par l’Allemand Hermann Schwarz (1843‒1921).

Le passage aux dimensions supérieures n’est pas aisé et nécessitera l’utilisation de la théorie algébrique des nombres et l’élaboration d’une géométrie des espaces convexes ainsi que l’appel à des nouvelles notions de topologie. Un théorème isopérimétrique général pour les géométries euclidiennes et la mesure de Lebesgue a été établi à la fin des années 1930 par l’Allemand Moritz Werner Fenchel (1905‒1988) et le Russe Alexandre Danilovitch Alexandrov (1912‒1999).