Calculer ? Avec des calculi, évidemment !

Nous calculons aujourd’hui avec les chiffres indo-arabes, une numération décimale et positionnelle, et à l’aide de méthodes qui nous viennent d’Inde. Attestées autour du VI^e siècle, ces méthodes sont décrites vers 825 à Bagdad par al-Khwarizmi, savant dont le nom latinisé a donné le mot « algorithme ». Mais avant, comment calculait-on ? Étonnamment, la question est difficile : en effet, le calcul quotidien, celui du commerce, a laissé peu de traces historiques ou archéologiques. Néanmoins, une réponse se dégage de ces recherches : on calculait avec des cailloux (en latin, des calculi) disposés sur des abaques. Explorons ce que l’on sait de ces objets dans les mondes mésopotamien, grec et romain notamment, en nous appuyant sur le site de l’association L’aventure du calcul (www.aventureducalcul.fr), qui doit beaucoup au sujet de ces abaques aux publications d’Alain Schärlig et Jérôme Gavin, des auteurs familiers des lecteurs de Tangente.

Les tables à poussière

En Mésopotamie, la numération sumérienne est l’une des plus anciennes décrites par les archéologues ; elle s’appuie sur des calculi de formes et de tailles différentes selon leurs valeurs. Adaptées à la base 60 qu’ils utilisaient pour calculer (base sexagésimale), ces valeurs étaient : 1, 10, 60, 600, 3 600, 36 000.

Les calculi servaient à noter les nombres et, peut-être également, aux opérations courantes. Faire des opérations revient alors à manipuler ces cailloux sur une table, probablement un abaque (ou abacus), étymologiquement une « table à poussière », à savoir une planche en bois couverte d’une fine couche de sable pour y tracer des caractères ou des traits de repérage. Malheureusement, si l’on dispose de nombreuses tablettes mésopotamiennes mathématiques en argile donnant des résultats d’exercices ou de problèmes, on a peu d’informations sur les méthodes de calcul qu’ils utilisaient.

Un scribe, un jour, a eu l’idée brillante de faire varier la valeur du caillou selon l’endroit sur lequel il le posait sur l’abaque, et non de fixer la valeur par la forme du calculus lui-même, comme dans le système sumérien. Les calculi deviennent ainsi des jetons banalisés qui prennent leur valeur en fonction du quadrillage porté par l’abaque. Là encore, ces abaques confectionnés « dans la poussière » ont laissé peu de traces archéologiques en Mésopotamie ou en Égypte ; heureusement, dans le monde grec, une trentaine d’exemplaires en pierre nous sont parvenus, dont celui de Salamine ! Dans un coin du marché, sur l’île de Salamine, un comptable faisait son office sur un tel abaque avec des calculi (ou psèphoï en grec).

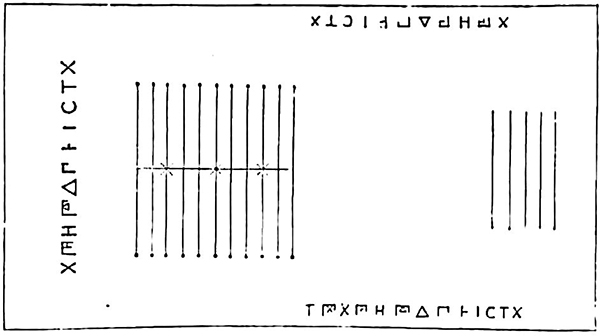
Représentation de l’abaque de Salamine (V^e siècle avant notre ère).

Même si nous n’avons pas le mode d’emploi de cet abaque dans les écrits antiques, les inscriptions qu’il contient nous permettent de le reconstituer. On sait que les Grecs utilisaient deux types de numération ; celle qui figure ici est dite acrophonique : elle s’appuie sur la première lettre du mot désignant chaque puissance de 10 et sur un signe pour leurs multiples de 5. Cette numération sera reprise et adaptée par les Romains (voir ci-dessus).

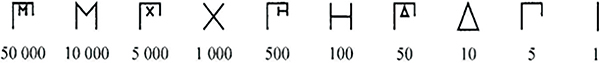
La notation grecque ci-dessus s’arrête à la myriade, symbolisée par M, qui vaut 10 000, ce qui devait être suffisant pour tous les calculs courants. L’inscription sur l’abaque de Salamine comporte, outre ces signes numériques, les signes ci-dessous pour les monnaies, ce qui conforte l’usage comptable de cet abaque.

Le signe ├ est celui de la drachme, la monnaie grecque. À gauche de ce symbole figurent les chiffres pour indiquer le nombre de drachmes jusqu’à 5 000. La dernière lettre à gauche sur cette liste, le T, correspond à un talent, qui valait six mille drachmes. Les indications à droite du symbole de la drachme correspondent à des subdivisions monétaires. L’unité principale (la drachme) se décomposait en six oboles. Les oboles sont comptées en unités avec les I, puis en demi-oboles (C), puis en quart d’oboles (T). Enfin, le X à droite représente la plus petite subdivision, le chalque. Une obole valait huit chalques, valeur qui a pu varier selon la région et l’époque. Le comptable et son client avaient ainsi sous les yeux tous les symboles nécessaires à leurs travaux.

Plusieurs dispositions de l’abaque sont possibles selon la façon de mettre en place les multiples de 5. Dans la première (ci-contre, en haut), on a une ligne séparant en partie haute des jetons quinaires et en partie basse des jetons unaires, ce qui donne une disposition proche des bouliers chinois ou japonais modernes. Dans la deuxième disposition (ci-contre, au centre), on trace des colonnes et les jetons posés sur les lignes sont unaires alors que les jetons posés entre les lignes sont quinaires. Enfin, dans une troisième disposition (ci-contre, en bas), on a un abaque développé, sur lequel on alterne les colonnes pour jetons unaires et les colonnes pour jetons quinaires.

C’est le nombre 3 648 qui a été écrit selon chacune de ces trois dispositions.

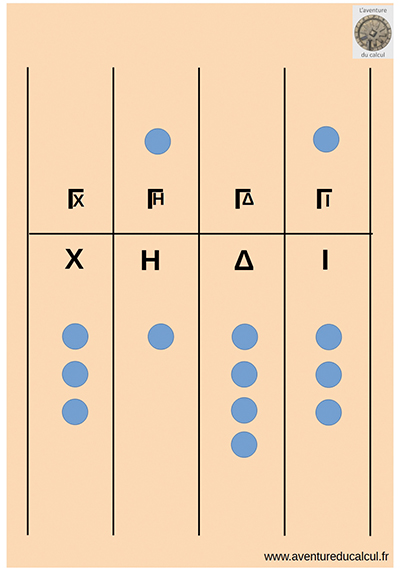
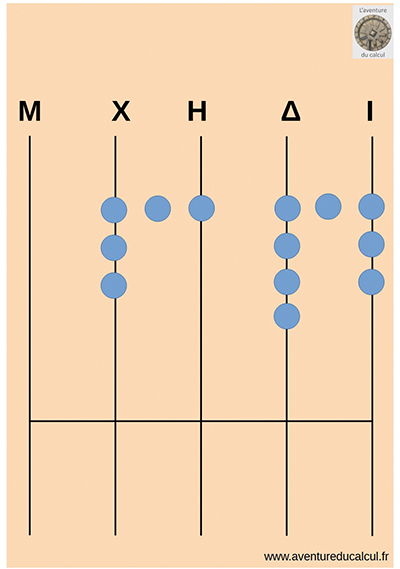
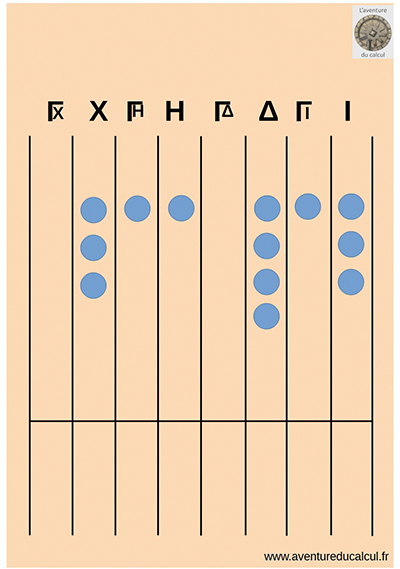
Exercice : lisez 3 648 sur ces abaques.

Les additions et les soustractions

Ces trois dispositions ont pu être adoptées, ainsi que des variantes verticales et horizontales, selon la région et l’époque. Dans tous les cas, additionner comporte les étapes suivantes :

• poser le premier nombre, puis le second nombre ;

• regrouper les jetons de même valeur ;

• réduire le nombre de jetons au minimum nécessaire en remplaçant, à chaque fois que possible, cinq jetons unaires par un jeton quinaire puis deux jetons quinaires par un jeton unaire de la puissance de 10 supérieure.

Le processus de réduction, décrit ci-dessus pour la base 10, est à adapter lorsque la base n’est pas 10 mais, par exemple, 6 comme dans le cas des oboles et des drachmes. La méthode de calcul pour la soustraction se décline facilement en remplaçant l’étape de réduction par une étape d’ampliation, où l’on échange autant que nécessaire un jeton qui vaut 10 par deux jetons qui valent 5, et un jeton qui vaut 5 par cinq jetons qui valent 1. Pour la multiplication, l’abaque sert à cumuler les résultats des produits partiels calculés en appliquant les tables de Pythagore (que les Mésopotamiens apprenaient déjà par cœur).

Les Romains ont repris des Grecs la numération acrophonique avec les chiffres romains qui sont restés les nôtres jusqu’à la Renaissance : I, V, X, L, C, D, M pour 1, 5, 10, 50, 100, 500, 1 000 respectivement. Ils ont également repris le principe des calculi, auxquels ils ont donné ce nom, ainsi que celui des abaques, comme on peut le déduire de la statuaire. Dans la scène ci-dessous, extraite d’un monument conservé à Trèves (Allemagne), deux personnages font face à une table avec des calculi alignés :

Par ailleurs, sur cet autre bas-relief du musée du Capitole à Rome (voir page suivante), on voit à gauche un esclave calculant sur son abaque sous la dictée du maître.

On dispose, à nouveau, de peu de sources écrites sur l’utilisation de ces calculi et abaques par les comptables romains, mais on peut suivre une règle assez simple, même si elle n’est qu’hypothétique : c’est qu’ils les utilisaient comme les Grecs, selon les mêmes méthodes, que l’on retrouvera d’ailleurs pendant tout le Moyen Âge en Europe (méthodes qui ont fait l’objet de nombreux ouvrages sur le « calcul à jetons » jusqu’au XVIII^e siècle).

Un proto-boulier ?

Les Romains ne se sont pas contentés d’adopter les méthodes héritées des Grecs : ils ont également innové et inventé, autour du I^er siècle de notre ère, ce que nous pouvons appeler un « proto-boulier ». En fixant les jetons unaires en bas et quinaires en haut, jetons qui coulissent dans des fentes, ils ont imaginé ce qui préfigure les bouliers chinois et japonais qui apparaîtront quelques siècles plus tard.

Reconstitution d’un « proto-boulier » romain.

Outre le boulier dans le monde asiatique, le calcul sur abaque a également eu une grande pérennité en Europe. Il est resté la norme pour les marchands pendant toute l’époque médiévale… et jusqu’au XVIII^e siècle ! Il était en particulier bien adapté aux calculs avec des unités composées non décimales. Sur des tables de compte, comme celle du musée du château de Thoune en Suisse (représentée ci-dessous), on reconnaît, de haut en bas : les lignes pour les milliers, centaines et dizaines de livres, en chiffres romains, et, au-dessous, trois lignes pour les sous (il faut vingt sous pour faire une livre) et, enfin, deux lignes pour les deniers (avec douze deniers pour faire un sou).

Ainsi, ces abaques à lignes ont permis de calculer de façon simple, malgré les subdivisions composées qui ont pullulé jusqu’à la Révolution française et l’adoption progressive du système décimal pour toutes les unités (monnaies, poids, volumes, longueurs, surfaces…).

Avec le calcul à jetons d’un côté et le boulier de l’autre, on a donc calculé avec les descendants des abaques et calculi mésopotamiens jusqu’à la fin du XX^e siècle, au moment où les calculettes électroniques à bas prix ont envahi le marché. Mais les abaques et les bouliers n’ont pas dit leur dernier mot, car le calcul concret avec ces instruments revient à l’ordre du jour, non pour les calculs du quotidien, mais pour leur intérêt pédagogique dans l’enseignement de la numération et du calcul à l’école et au collège !