
Un ensemble (de préférence fini) d’objets écrits dans un certain ordre étant donné, modifions l’ordre de ses éléments sans en ajouter ni en retirer : le résultat ainsi obtenu s’appelle une permutation.
Les permutations ont commencé à attirer l’attention des mathématiciens notamment dans les années 1770, avec les travaux d’Edward Waring (1736-1798) et d’Alexandre-Théophile Vandermonde (1735-1796), car elles permettent d’étudier les racines d’une équation algébrique. Mais c’est Joseph-Louis Lagrange (1736-1813) qui, posant les bases de ce qui deviendra la théorie de Galois, a mis en place une première théorie des permutations.
Au début du XIXe siècle, celle-ci progresse avec Paolo Ruffini (1765-1822)… et Cauchy.
Mémoire de valeurs
Sans être particulièrement intéressé par l’étude des équations algébriques, Cauchy étudie néanmoins les permutations dans le cadre d’un problème de théorie des nombres (le théorème de Fermat sur les nombres polygonaux). Reprenant une lecture faite sur le sujet à l’Académie en 1812, il publie en 1815 deux mémoires dans le Journal de l’École polytechnique.
Dans le premier, intitulé Sur le nombre des valeurs qu’une fonction peut acquérir, lorsqu’on y permute de toutes les manières possibles les quantités qu’elle contient, Cauchy commence par redémontrer un résultat de Lagrange. Son apport est jugé suffisamment important pour que Camille Jordan, énonçant ce résultat sous une forme plus générale en 1870, lui attribue le nom de Cauchy-Lagrange (voir encadré ci-dessous).
Le théorème de Cauchy-Lagrange
Soit H un sous-groupe du groupe fini G. On note xH l’ensemble des éléments de G qui peuvent s’écrire sous la forme xh, où h est un élément de H. En quelque sorte, donc, xH est une copie de H « décalée » d’un facteur x. Le sous-groupe H étant fixé, le nombre d’éléments (on parle plutôt d’ordre) de xH , noté |xH|, est le même quel que soit x. D’autre part, si y est un élément de G qui n’est pas dans xH, alors xH et yH sont disjoints. En effet, s’ils avaient un élément z en commun, on pourrait écrire z à la fois sous la forme xh et sous la forme yh’ pour certains éléments h et h’ de H, et on aurait donc yh = xh’, et donc y = x(h’h-1). Or puisque H est un groupe on devrait avoir que h’h- 1 ∈ H, et donc y ∈ xH.
Nous avons donc montré que les ensembles distincts de la forme xH sont deux à deux disjoints. D’autre part, leur réunion est égale à G tout entier (car tout élément x de G appartient à xH, en vertu de l’égalité x = xe où e est l’élément neutre de G, qui est nécessairement dans H puisque H est un sous-groupe). Les xH constituent donc une partition de G, que l’on note G:H pour évoquer une « division ».
Puisque tous les xH ont le même nombre d’éléments, le nombre d’éléments de G est égal au nombre d’éléments de G:H multiplié par le nombre d’éléments de chaque classe. On en déduit le théorème de Lagrange : le nombre d’éléments d’un sous-groupe H de G est un diviseur du nombre d’éléments de G.
Beaucoup de notions que Cauchy définit et dénomme seront adoptées par ses successeurs. Il établit une claire distinction entre une permutation, qui est un arrangement quelconque de n objets (par exemple {1, 2, 4, 3}, avec l’ensemble des entiers de 1 à 4), et une substitution, qui est le passage d’une permutation à une autre.
Par exemple, la substitution qui fait passer de {1, 2, 4, 3} à {2, 4, 3, 1} est notée
par Cauchy, une notation toujours en usage aujourd’hui.
Cauchy définit également ce qu’il appelle le produit de deux substitutions (et que nous appelons plutôt composition) : par définition, le produit S∙T des substitutions S et T est la substitution obtenue en appliquant S puis T ‒ Cauchy, puis Galois après lui, le font dans cet ordre ; par la suite, l’ordre sera inversé. Par exemple, si S est la substitution faisant passer de la permutation P1 à la permutation P2 et T celle qui fait passer de P2 à P3, alors S∙T est la substitution qui fait passer de P1 à P3. En revanche, si Cauchy utilise souvent le terme de « groupe », ce n’est que dans une acception ensembliste, et non avec la structure de groupe qui deviendra par la suite un pilier de l’algèbre.
Le théorème principal du premier article est ainsi énoncé :
Le nombre de valeurs différentes
d’une fonction de n quantités
ne peut s’abaisser au-dessous
du plus grand nombre premier p
contenu dans n sans devenir égal à 2.
Pour le démontrer, Cauchy introduit le concept de transposition, une permutation qui intervertit deux termes, de groupe cyclique et de substitution circulaire, et fait remarquer que toute permutation paire est un produit de 3-cycles (voir encadré ci-contre).
Cycles et transpositions
Considérons la permutation
Comme on le voit en représentant σ par le diagramme suivant
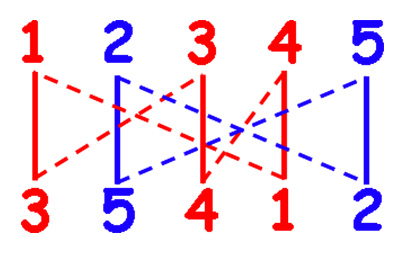
lorsqu’on répète la permutation encore et encore, les nombres finissent par se répartir en deux blocs (un rouge et un bleu), qui constituent des cycles. C’est ainsi que σ est le produit du cycle (1,3,4) et du cycle (2,5). On peut démontrer que toute permutation peut être décomposée en cycles.
Une permutation qui n’est composée que d’un seul cycle est dite circulaire.
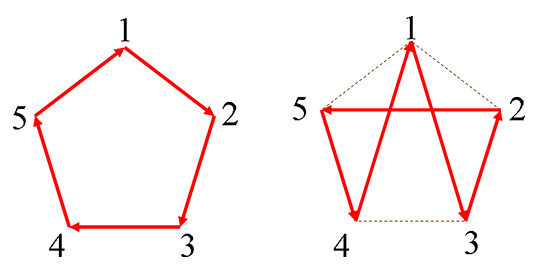
Les permutations
 et
et  ,
,
toutes deux circulaires.
Cauchy appelle transposition un cycle à deux éléments, une dénomination toujours utilisée aujourd’hui. L’importance des transpositions tient au fait que toute permutation se décompose en produit de transpositions. Cette décomposition n’est pas unique, mais la parité du nombre de transpositions est, elle, toujours la même pour une permutation σ donnée. La signature de σ est définie par la valeur +1 lorsque le nombre de transpositions est pair, et par la valeur -1 lorsqu’il est impair.
Mémoire déterminant
Dans son second article, Mémoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et de signes contraires par suite des transpositions opérées entre les variables qu’elles contiennent, Cauchy introduit de nouvelles notions, appelées à jouer un rôle essentiel dans ce qui deviendra l’algèbre linéaire. Il y développe notamment la notion de déterminant, et en donne les principales propriétés, notamment la règle de leur développement selon les lignes et les colonnes et, surtout, que le déterminant d’un produit est égal au produit des déterminants.
Ces deux premiers textes préfigurent le style mathématique de Cauchy et dessinent déjà les contours conceptuels, encore flous, dans lesquels la théorie des substitutions deviendra la théorie des groupes.
références
•
Les travaux de Cauchy sur les substitutions. Etude de son approche
du concept de groupe, Amy Dahan, Archive for History of Exact Sciences, Springer-Verlag, 1980.
• Évariste Galois,
Bibliothèque Tangente 82, POLE, 2023.
• Les groupes,
Bibliothèque Tangente 80, POLE, 2022.


