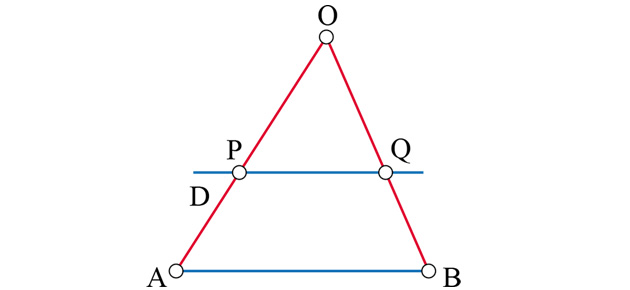
Dans sa version classique, le théorème de Thalès est un théorème de géométrie plane. Un triangle OAB et une droite D parallèle au côté [AB] sont donnés. La droite D coupe les deux côtés [OA] et [OB] en deux points, P et Q.
Le théorème de Thalès fournit alors la relation numérique suivante :
La méthode la plus simple pour démontrer cette égalité fait intervenir les aires de certains triangles. Elle utilise un lemme concernant deux triangles OAB et OBC construits sur une même droite (ABC). Ils possèdent la même hauteur (OH).
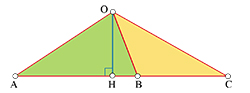
Leurs aires sont égales à la moitié des produits de OH par AB et BC, donc :
Ce résultat est valable dans toutes les configurations identiques, en particulier pour les triangles QOP et QPA d'une part et QOP et PQB d'autre part. On peut ainsi écrire :
Comme les deux triangles QPA et QPB ont la même base (PQ) et la même hauteur (la distance entre les deux droites (PQ) et (AB)), ils ont même surface. Les rapports d'aires sont donc égaux : Le reste ... Lire la suite gratuitement
