
Pour déterminer le plus court chemin d'un point à un autre sur un plan, il suffit de disposer d'une règle et de tracer la droite qui les joint. Le problème n'est pas plus compliqué dans le cas des surfaces développables, qui, comme les cylindres, les cônes ou le ruban de Möbius, peuvent être mis à plat sans déchirement ni étirement, donc sans que les distances soient modifiées. Pour déterminer le plus court chemin, il suffit d'« aplatir » la surface et de tirer un trait avec une règle.
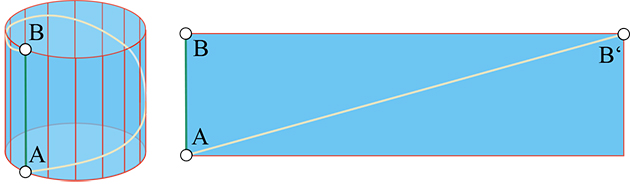
Aplatissement d'un cylindre pour déterminer ses géodésiques. On obtient des cercles (les directrices, en orange), des hélices (en jaune), et des droites (les génératrices, en rouge).
Dans le cas du cylindre, chaque point peut être représenté plusieurs fois, ce qui donne plusieurs courbes possibles a priori. Toutes sont appelées des géodésiques, même si une seule d'entre elles réalise le plus court chemin, car elles ont une propriété commune. Elles correspondent aux positions que prend un élastique tendu entre les deux points, à condition que la surface soit ... Lire la suite
