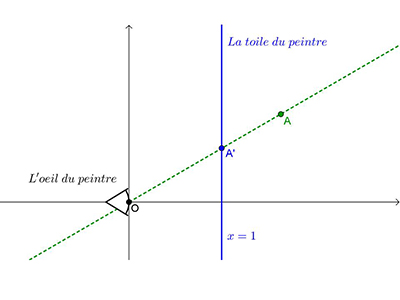
 Admirons le peintre de la Renaissance à son ouvrage. Imaginons cette situation représentée de profil dans le plan muni d'un repère orthonormé. Comme sur le schéma ci-dessous, on peut imaginer que l'œil de l'artiste est situé en l'origine et que la toile du maître est située sur la droite d'équation x = 1, parallèle à l'axe des ordonnées.
Admirons le peintre de la Renaissance à son ouvrage. Imaginons cette situation représentée de profil dans le plan muni d'un repère orthonormé. Comme sur le schéma ci-dessous, on peut imaginer que l'œil de l'artiste est situé en l'origine et que la toile du maître est située sur la droite d'équation x = 1, parallèle à l'axe des ordonnées.
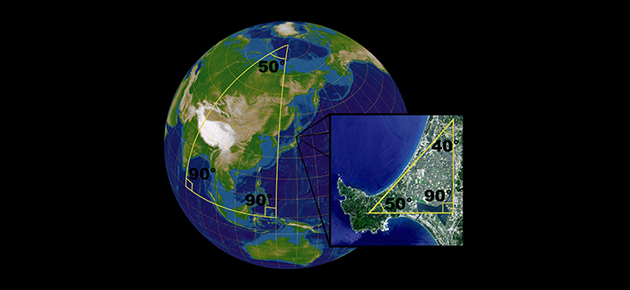
Si la toile est infinie, tout point A du plan peut être projeté sur un point A' de la toile. On peut même observer que tous les points situés sur une même droite passant par O sont projetés sur le même point de la toile. Ainsi, toute droite du plan passant par l'origine correspond à un unique point de la droite d'équation x = 1. Toutes ? Non ! Une droite résiste encore : l'axe des ordonnées. Qu'à cela ne tienne, ajoutons un nouveau point à notre droite-toile : un point « à l'infini », qui correspond intuitivement à l'endroit où se couperaient l'axe des ordonnées et la droite d'équation x = 1. Et c'est ainsi que les travaux des peintres sur la perspective nous offrent un nouveau point de vue sur la géométrie du plan !
Un nouveau point… de vue
Plus généralement, si l'on considère un plan vectoriel E, la droite projective ... Lire la suite
