
« Jamais le soleil ne voit l'ombre » disait Léonard de Vinci, preuve déjà que la notion d'ombre avait son importance à son époque. C'est d'ailleurs bien avant lui que cette notion a pris de la valeur puisqu'elle a été utilisée pour mesurer les hauteurs inaccessibles : les géomètres de l'Antiquité avaient compris que voir l'ombre d'un objet, c'est déjà avoir une idée de ses dimensions. L'ombre s'est faite à la Renaissance instrument des théoriciens de la perspective, certains que voir l'ombre d'un objet, c'est déjà un peu le reconnaître, et du coup savoir le dessiner avec l'illusion du réel, nous dirions aujourd'hui « en 3D ».
Quelques siècles plus tard, c'est l'ombre « propre » des objets qu'ont utilisée les informaticiens pour rendre sur écran le relief des choses : qui a oublié la fameuse « théière de l'Utah » créée en 1975 par Martin Newell, devenue un véritable objet culte dans l'univers de l'informatique graphique ? La notion d'ombre a donc sur notre environnement spatial une grande influence.
.jpg)
Un célèbre modèle d'infographie : la théière de l'Utah.
L'ombre au soleil
Utiliser l'ombre projetée par le soleil pour mesurer des distances inaccessibles est une vieille histoire, qui remonte environ au VIe siècle avant notre ère. De nombreuses sources attestent en effet que Thalès, non seulement avait voyagé en Égypte, mais avait mesuré la hauteur des pyramides « en observant la longueur de leur ombre au moment où notre ombre est égale à notre propre hauteur ». Le procédé ? Partant du principe que les rayons du soleil sont parallèles, utiliser des triangles, que l'on nommera semblables par la suite. La méthode ? Montrer, selon Plutarque, « en plantant un bâton à l'extrémité de l'ombre de la pyramide et en créant deux triangles par l'impact des rayons du soleil, que la pyramide avait au bâton le même rapport que l'ombre de la pyramide à l'ombre du bâton ». Tous calculs faits, cela donne :
.jpg)
Les rayons solaires étant considérés comme parallèles, l'ombre est exactement l'image d'un objet par projection parallèle sur le sol, ce qui n'est rien d'autre que son dessin en perspective parallèle. Connaître une ombre, c'est déjà savoir passer de l'espace au plan, donc dessiner en perspective. L'ombre d'un segment est toujours un segment et les milieux sont conservés. Le dessin s'opère ainsi tout naturellement.
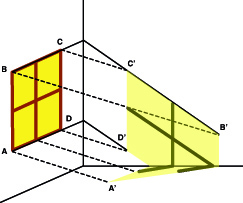
Le soleil entre par la fenêtre. La fenêtre à carreaux ABCD projette sur le mur d'à côté sa lumière A'B'C'D' dont les montants des carreaux font une ombre.
L'ombre au flambeau
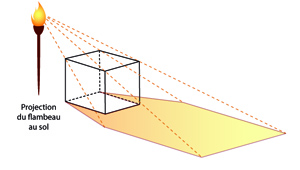
Pour l'ombre dite au flambeau, c'est différent car les rayons lumineux sont ici tous issus d'un même point, le flambeau, mais savoir dessiner l'ombre projetée dans ces conditions c'est savoir dessiner une image par projection centrale. La situation de l'ombre au flambeau est donc exactement celle de la perspective centrale, que Dürer (1471-1528) illustra si bien par son dispositif appelé fenêtre de Dürer, où un oeilleton fixe la place de l'oeil de l'opérateur, une fenêtre étant placée entre cet œil et l'objet à représenter. Tout point de cet objet est représenté par l'intersection avec le plan de la fenêtre du rayon lumineux joignant ce point à l'oeil, tout comme l'ombre d'un point est l'intersection du rayon issu du flambeau et passant par ce point avec le plan de l'écran (le mur ou le sol, ou toute autre surface plane) sur lequel sera projetée l'ombre.
Les techniques du dessin d'ombre, qui amènent à « aplatir » en deux dimensions un objet donné en trois dimensions, sont donc aussi celles du dessin en perspective : on gagne toujours à savoir tirer (des traits) plus vite que son ombre…
Le carré des ombres
Le carré des ombres est un instrument de topographie, souvent gravé au dos des astrolabes, utilisé à partir du IXe siècle. C'est chez al-Khwarizmi qu'on en trouve la première mention dans la littérature. Il s'agit bel et bien d'un carré, et c'est par analogie avec les mesures de hauteur effectuées avec l'ombre d'un bâton qu'on lui a donné ce nom.

Comment utiliser le carré des ombres ? Sur cette illustration, le carré des ombres peut être utilisé par un observateur qui souhaite connaître la hauteur d'une tour. Les côtés sont tous divisés en douze parties égales. On se place à une distance connue du pied de la tour et on pointe le sommet avec le carré des ombres. On reproduit ainsi un triangle rectangle dont les proportions sont semblables à celles du triangle que forment l'impact de l'observateur au sol, la tour et la direction de visée. Tant que l'angle de visée est inférieur à 45°, on utilise l'échelle verticale (verse), s'il est plus grand, l'échelle horizontale (recte). Sur l'image, l'angle de visée est inférieur à 45°. L'observateur, à 120 pas du pied de la tour, voit une ombre verse de 10 (sur 12). C'est dire que la hauteur de la tour est de 10/12e de la distance de 120 pas : cette tour a donc une hauteur de 100 pas.
Références : Les angles. Bibliothèque Tangente 53, 2015.
Discours de l'ombre
Le mot « ombre », élément structurant de notre vision de l'espace, est aussi très présent dans notre discours et nombreuses sont les expressions de notre langue qui l'intègrent. Combien en dénombrez-vous dans ce petit texte ?
« Pour chercher cette location de vacances, autrement dit, un coin d'ombre pour l'été, tu as, sans l'ombre d'un doute, lâché la proie pour l'ombre et abandonné ton confortable appartement pour un problématique studio en bord de mer avec terrasse ombragée. Seule ombre au tableau : le propriétaire, vivant certainement dans l'ombre de malfrats, vient d'être mis à l'ombre… Voilà donc ses combines débusquées, comme sorties de l'ombre, mais toi ? Et les arrhes que tu avais versées dans l'ombre ? Vouloir les récupérer, c'est courir après son ombre. Et le mandataire énervé du proprio indélicat, cet ombrageux personnage, tu n'aimes sans doute pas qu'il te fasse de l'ombre ! Je te vois d'ici passer comme une ombre sous ses fenêtres, des idées de revanche plein la tête. Déjà, tu n'es plus que l'ombre de toi-même ; inutile de te la jouer dans ton théâtre d'ombres, toi qui avais déjà peur de ton ombre… Alors, rentre chez toi et… marche à l'ombre ! »
