
Le théorème connu de nos jours sous le nom de « théorème de Pythagore » apparaît dans sa forme définitive, pour ce qui concerne la géométrie plane, comme la proposition 47 du livre I des Éléments d'Euclide : dans tout triangle rectangle, le carré construit sur l'hypoténuse est équivalent à (de même aire que) la somme des carrés construits sur les côtés perpendiculaires.
La proposition suivante (numéro 48) est sa réciproque : l'égalité des carrés implique que le triangle est rectangle. À aucun moment, Euclide n'associe le nom de Pythagore à ces deux propositions. Le texte contient une démonstration générale, illustrée par une figure chez Euclide, traduite ici en trois schémas. La démarche consiste à découper le carré construit sur l'hypoténuse en deux rectangles dont chacun a une aire égale à celle de l'un des carrés construits sur les côtés de l'angle droit.
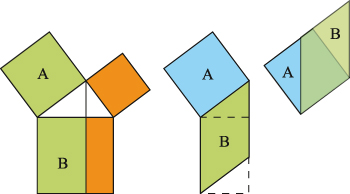
Il suffit de démontrer que A = B, l'autre égalité s'ensuivant par symétrie. Les deux transformations (à droite) de la partie B permettent de le prouver.
