
Voici une situation mathématique bien courante : soit f une fonction continue et monotone (c’est-à-dire croissante ou décroissante) définie entre deux réels a et b, telle que f (a) et f (b) soient de signe contraire. Comme f est continue, elle croise mécaniquement l’axe des abscisses (c’est le théorème des valeurs intermédiaires). Comme en outre elle est monotone (ici, croissante), il n’y a qu’une seule solution à l’équation f (x) = 0. On l’appelle racine de l’équation et on la note α.
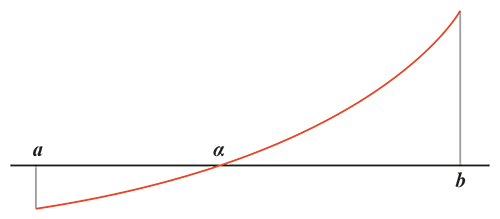
Dans certains cas, par exemple si f (x) est un trinôme, c’est-à-dire un polynôme du second degré, il existe des formules, bien connues des lycéens, pour donner la valeur de α. Mais, en général, pour une expression f (x) quelconque, il n’existe pas de méthode exacte pour trouver cette valeur. Par contre, il existe des méthodes itératives pour trouver une valeur approchée de α. Voyons les plus connues.
En divisant l’intervalle
La première méthode s’appelle méthode par dichotomie. Derrière ce mot un peu savant se cache l’idée, toute simple, que l’on va partager l’intervalle [a, b] en deux morceaux de même longueur et regarder dans quel morceau se trouve la racine α. Ce nouvel intervalle sera de longueur moitié par rapport à l’intervalle ... Lire la suite
