
L’OEIS : quésaco ?
L’OEIS (On-line Encyclopedia of Integer Sequences) est une encyclopédie en ligne des suites d’entiers répertoriant, à ce jour, plus de trois cent mille suites. Entrez quatre ou cinq termes consécutifs (des nombres entiers), et vous obtiendrez toutes les suites (finies ou infinies) répertoriées contenant cette séquence. Pour chaque suite, vous trouverez diverses définitions, des propriétés, des formules, des exemples de constructions de termes, des références (papier ou Internet), ainsi que des programmes de calcul de ses termes dans différents langages informatiques.
Une suite de rationnels est répertoriée par la suite de ses dénominateurs et celle de ses numérateurs. L’OEIS est aussi une encyclopédie des constantes mathématiques, par le biais des suites de leurs décimales. Le moteur de recherche, très efficace, permet aussi de faire une recherche sur des mots.
Neil James Alexander Sloane, mathématicien américano-britannique spécialiste de combinatoire né en 1939, est le fondateur de cette encyclopédie. Même si le site est maintenant géré par une fondation, Neil Sloane y est toujours actif.
Quelques exemples
Une recherche sur le terme « Fibonacci » dans l’OEIS ne vous donnera pas seulement la suite du même nom (elle apparaîtra tout de même en premier : A000045), mais neuf mille cinq cent vingt-huit exemples à ce jour !
Vous découvrirez par exemple le mot infini de Fibonacci (A003849) : 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0… (partir de 0, puis appliquer à l’infini la transformation 0 → 01, 1 → 0).
Une recherche sur la chaîne de caractères « look and say » vous donnera la suite audioactive de Conway (A003849) 1, 11, 21, 1211, 111221, 312211…, dont le terme suivant est la lecture des chiffres du terme précédent (voir Tangente 191, 2019), mais aussi cent vingt-quatre variantes ! Attention, les mots séparés « look » « and » « say » vous donneront deux cent onze suites, bien sûr incluant les précédentes.
Le saviez-vous ?
La première entrée de l’OEIS, la suite A000001, donne le nombre de groupes d’ordre n.
Il faut attendre A000027 pour avoir les entiers strictement positifs, A001477 pour avoir les entiers positifs ou nuls, A005843 pour les entiers pairs, A005408 pour les entiers impairs. Les nombres premiers, eux, forment la suite A000040.
La suite Q de Hofstadter (A005185) est telle qu’on ne sait pas si elle est définie pour tout entier.
La suite de Gijswijt (A090822) croît très lentement : le premier terme égal à 5 n’apparaît qu’à la 1010 23ème place !
Il existe une suite des cure-dents (A139250), qu’un enfant peut comprendre.
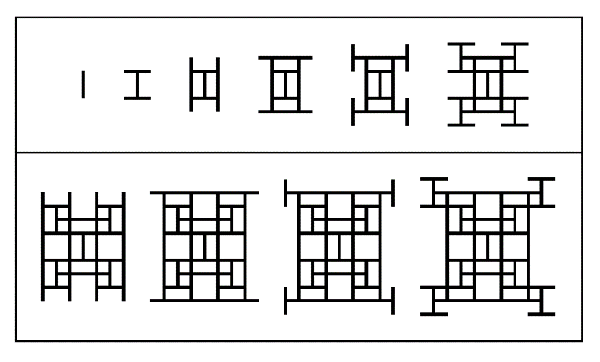
Les dix premières étapes de la construction de la suite des cure-dents :
1, 3, 7, 11, 15, 23, 35, 43, 47, 55.
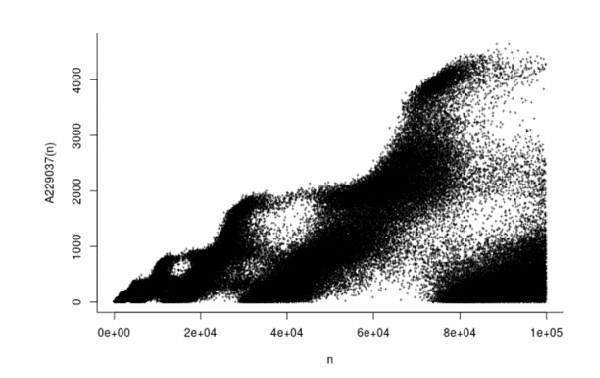
La suite de la forêt en flamme porte le numéro A229037.
Une encyclopédie vivante
Tous les jours, de nouvelles suites sont introduites sur le site. Si, vous-mêmes, vous voulez ajouter des informations, il faudra vous inscrire et vous connecter. Vous pourrez alors ajouter une suite inconnue, si possible en donnant une cinquantaine de termes et en donnant la propriété caractéristique. Si vous modifiez une suite préexistante, vous devrez ajouter vos commentaires (en anglais) après ceux des autres et les signer. Cela fait que pour les suites très classiques (comme celle de Fibonacci) les commentaires, nombreux, ne sont pas du tout classés et donnent un peu une impression de fouillis…
Tout est en mode texte, donc pas forcément agréable (ni à écrire, ni à lire). La validation par un éditeur autorisé des modifications proposées demande parfois un peu de temps et vous ne pouvez pas créer ou modifier plus de trois suites tant que vos propositions précédentes n’ont pas été validées.
Cette encyclopédie est malgré tout extrêmement précieuse : c’est véritablement LA référence incontournable sur les suites !
