
La première trace du théorème de Pythagore apparaît dans le cas particulier du triangle rectangle isocèle en Mésopotamie voici quatre mille ans. Bien plus tard, Platon (428–348 avant notre ère) reprend ce cas dans Le Ménon. Socrate y décrit la figure suivante, qu’on l’imagine avoir tracée sur le sable.
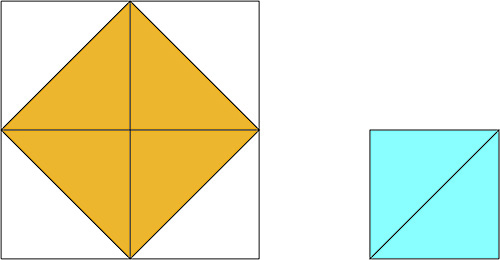
En comptant les triangles, on montre que la surface du carré (en biais, de couleur ocre) construit sur les hypoténuses des triangles est le double de celle des petits carrés (dont une copie est en bleu).
À partir de là, il est effectivement facile de montrer que l’aire du grand carré est le double de celle du carré de biais. Cette figure nous fait osciller dans le temps de plus d’un millénaire, entre la Grèce et la Mésopotamie. Entre Platon et une tablette d’argile pouvant tenir dans la paume de la main, probablement un travail d’étudiant selon les archéologues, un exercice à résoudre contenant un énoncé et un résultat comme toutes les autres tablettes à caractère mathématique retrouvées en Mésopotamie.

Tablette YBC 7289 (« YBC » pour « Yale Babylonian Collection »)
conservée à l’université de Yale, aux États-Unis.
On y voit un carré divisé en quatre triangles rectangles ... Lire la suite
