
Philippe Carmona et Sylvain Gandon, du Centre national de la recherche scientifique (CNRS), ont développé un modèle mathématique pour expliquer ce phénomène. Leurs travaux mettent en évidence l’existence d’un « hiver » pour les pathogènes dits saisonniers. Il s’agit d’une période pendant laquelle ils se transmettent moins vite qu’ils ne disparaissent au sein de la population (figure du dessus), limitant ainsi le risque d’une épidémie importante. Les chercheurs ont démontré que le risque épidémique pour un pathogène donné dépend de son moment d’introduction : si le pathogène apparaît pendant son « hiver » ou peu avant, ce risque est considérablement réduit (figure du dessous). C’est l’effet « winter is coming ». Ainsi, la probabilité de vivre une épidémie de grippe au mois d’août en France est quasiment nulle. Comprendre cette dynamique saisonnière devrait favoriser la lutte contre les épidémies : agir au bon moment contre un pathogène pourrait aider à limiter sa propagation.
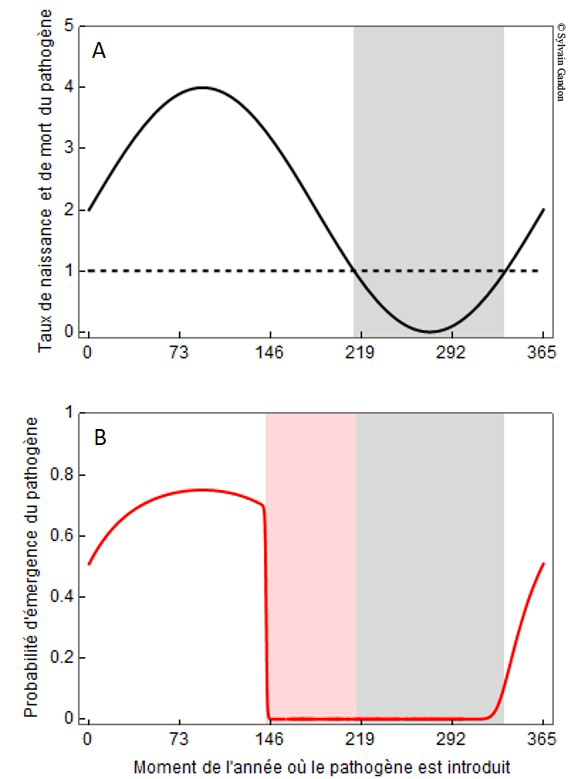
La figure du dessus montre la variation du taux de naissance (taux de transmission du pathogène, trait plein) et de mort (taux de guérison de l’hôte infecté par le pathogène, trait pointillé) au cours du temps (l’unité de temps est le jour). La zone en gris foncé représente l’« hiver » pour le parasite (en « hiver » le taux de naissance est plus faible que le taux de mort). La figure du dessous montre la probabilité d’émergence du pathogène (courbe rouge) en fonction du jour de l’année où il est introduit. On voit que cette probabilité est très faible en « hiver » (taux de transmission faible) mais également juste avant l’hiver (zone rouge). Cette diminution très importante de la probabilité d’émergence pile avant l’hiver est l’effet « winter is coming ».
