
Prenez un segment. Quelles sont les transformations géométriques planes qui le laissent invariant, c’est-à-dire qui ne le modifient pas ? On trouve la symétrie d’axe la droite portant ce segment (notée SD), qui le laisse invariant point par point, et la symétrie d’axe la médiatrice du segment (notée SM), qui échange ses points et le laisse globalement invariant.
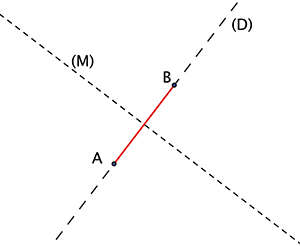
Que se passe-t-il quand on les compose (loi notée ), c’est-à-dire que l’on enchaîne ces transformations ? On peut alors résumer la situation dans la table ci-dessous, dite table de Pythagore de la loi.
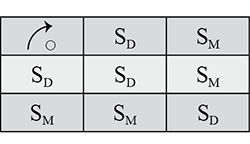
Avec des nombres, maintenant
Sortons de la géométrie pour nous intéresser à des objets complètement différents des figures : les nombres. Prenez les entiers. Ils peuvent être pairs ou impairs. Que se passe-t-il quand on les additionne ? On peut résumer les différents cas dans la table ci-dessous.
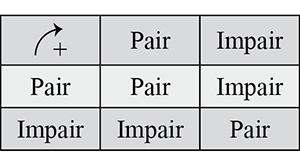
Regardez les deux tables obtenues avec ces deux exemples élémentaires mais bien distincts : aux notations près, elles se « ressemblent beaucoup » alors que les objets sont, pour l’un, {SD, SM} et, pour l’autre, {Pair, Impair} ! Autrement dit, les objets sont différents mais les relations entre eux sont identiques. Ces tables décrivent une structure. Par exemple, dans la seconde, ... Lire la suite
