
Tout commence par des sudokus ! De fait, lorsque l’on dresse la table d’un groupe fini, on constate que tous les éléments du groupe apparaissent une fois et une seule dans chaque ligne et chaque colonne. En effet, toute simplification est permise dans un groupe. En notant * la loi, on a les propriétés suivantes :
x * y = x * z implique y = z (propriété relative aux lignes de la table du groupe),
et y * x = z * x implique y = z (propriété relative aux colonnes de la table du groupe).
Cela revient à dire qu’il ne peut y avoir de répétitions dans une même ligne de la table du groupe, et de même pour chaque colonne.
Des carrés latins
Cette propriété de simplification aide grandement au remplissage de la table, surtout pour les habitués des sudokus (appelés plutôt carrés latins par les mathématiciens). Malheureusement, même s’il y a un élément neutre et que tout élément est simplifiable, cela ne suffit pas pour faire un groupe, comme le montre l’exemple classique ci-dessous, qui fait intervenir une loi de composition interne * ainsi que cinq objets différents a, b, c, d et l’élément neutre e.
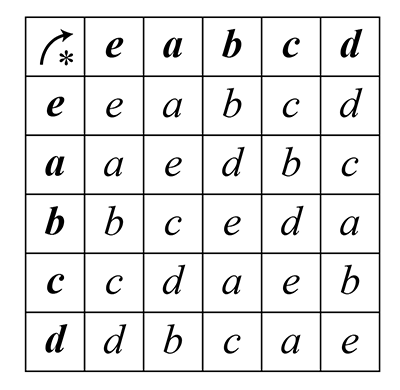
Calculez en effet (a * b) * c et a * (b * c) : la ... Lire la suite
