Un groupe fini est entièrement défini par sa table. Si l’ordre du groupe est n, la table comprend n2 cases. Il n’est pas évident, dès que n n’est « plus trop petit », de repérer des structures dans une telle table. De nombreux groupes possèdent un ou plusieurs générateurs c’est-à-dire un sous-ensemble du groupe dont les différentes combinaisons, via la loi de groupe, vont générer tous les éléments du groupe. Dans ce cas, le mathématicien britannique Arthur Cayley (1821−1895) utilise un graphe pour représenter le groupe : le diagramme de Cayley.
Il utilise même des couleurs pour distinguer les générateurs. Bien sûr, un groupe donné peut posséder plusieurs diagrammes, selon les générateurs choisis.
Des graphes et des générateurs
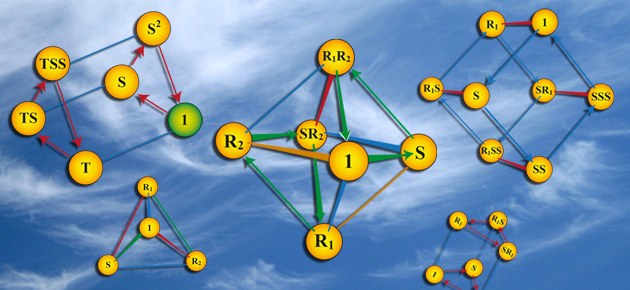
Un diagramme de Cayley est un graphe orienté dont les sommets sont les éléments du groupe et les arêtes sont les générateurs. Pour chaque sommet, il existe deux arêtes par générateur, une qui arrive et une qui part. Si le sommet V est relié au sommet W par l’arête orientée S, cela signifie que W = SV, en notant la loi du groupe de manière multiplicative, comme l’ont fait Cayley, puis William Burnside (1852−1927) et Harold Scott MacDonald Coxeter (1907−2003) après lui.
