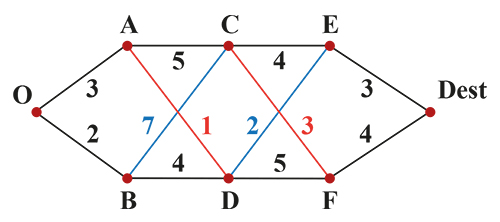
Pour commencer, il faut modéliser le réseau routier par un graphe G, à savoir un ensemble de sommets et d’arêtes : chaque intersection entre deux routes est un sommet de G, et chaque portion de route entre deux intersections est une arête. On peut donner une valeur (par exemple une distance en kilomètres ou en heures) à chaque arête, pour avoir un graphe valué. Trouver le plus court chemin entre deux sommets (une origine O et une destination Dest) consiste alors à trouver la succession d’arêtes reliant O à Dest de somme minimale.
En 1959, l’informaticien néerlandais Edsger Dijkstra a proposé un algorithme très efficace pour cela. Il utilise le principe énoncé par le mathématicien Richard Bellman, selon lequel tout sous-chemin du chemin optimal est lui-même optimal.
Autrement dit, si le plus court chemin de O à Dest est O-A-D-E-Dest, alors le plus court chemin de A à E est A-D-E… et réciproquement. Il est donc possible de trouver le plus court chemin entre l’origine et la destination en progressant sommet après sommet dans le graphe et en gardant en mémoire, à chaque itération, le plus court chemin reliant l’origine à chaque point du graphe.