
Un problème de géométrie métrique non résolu
La question a été posée en 1950, quand il était étudiant, par le mathématicien américain Edward Nelson (1932–2014), connu pour ses travaux en logique et en analyse non standard. Elle a aussi été introduite, sous une forme légèrement différente et de manière indépendante, par le mathématicien suisse Hugo Hadwiger (1908–1981), d’où son nom de problème d’Hadwiger–Nelson.
C’était l’un des sujets favoris de Paul Erdős, qui le citait souvent dans ses conférences en regrettant de ne pas l’avoir posé lui-même ! Le problème a par ailleurs été popularisé par Martin Gardner en 1960 dans sa chronique de la revue Scientific American.
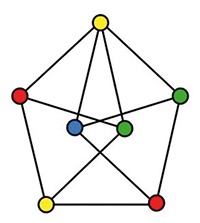
Ce nombre c de couleurs est souvent appelé le nombre chromatique du plan. Il est au moins égal à 4, qui est le nombre de couleurs nécessaires, en respectant la contrainte, pour colorier l’ensemble ci-dessous de points, où le segment tracé entre certains d’entre eux indique que leur distance mutuelle est égale à 1 (voir Tangente 195, 2020).
De même, il est tout aussi facile de montrer que sept couleurs sont suffisantes, en prenant un pavage du plan par des hexagones réguliers de côté strictement compris entre ... Lire la suite
