
Comment savoir qu’une étoile est « plus grande » que la Lune ? En constatant qu’elle est « beaucoup » plus éloignée ! Mais on ne peut pas sortir son mètre ruban et le tendre pour mesurer la distance entre les objets célestes. Il faut ruser, et procéder de proche en proche. On détermine d’abord la distance d’un objet relativement proche. Puis on utilise cette connaissance pour en déduire la distance d’un objet un peu plus lointain. On appelle ce principe l’échelle des distances : à chaque échelon, on se tient sur le barreau d’échelle précédent pour attraper le barreau suivant. Le premier échelon sur l’échelle des distances est le diamètre de la Terre.
Le diamètre de la Terre
Le premier écrit connu concernant la rotondité de la Terre est le Rig-Veda, un texte sacré hindou datant d’environ 1500 ans avant notre ère.
En Grèce antique, Aristote (–384 ; –322) a démontré que la Terre est ronde en observant la forme de l’ombre de la Terre pendant les éclipses lunaires.
Bref, pour Ératosthène (vers –276 ; vers –194), cela ne faisait aucun doute que la Terre est ronde. Sachant cela, il s’est mis en tête d’en mesurer la circonférence.
Il y aurait eu à Syène, au sud de l’Égypte moderne, un puits dont le fond était éclairé par le Soleil à midi le jour du solstice d’été. En supposant que le puits était creusé à la verticale, le Soleil se trouvait donc au zénith à midi. En fait, Syène se situe sur le vingt-quatrième parallèle, donc pas tout à fait sur le tropique, mais pas loin.
Ératosthène a estimé que la ville d’Alexandrie, au nord de l’Égypte, est sur le même méridien que Syène. Le jour du solstice, il a utilisé un gnomon (un bâton rectiligne planté verticalement, dont on peut suivre et mesurer au sol l’ombre) pour déterminer l’angle que faisait le Soleil avec la verticale. Il a ainsi mesuré un angle de 7°.
Si l’on suppose que le Soleil S est « infiniment loin » de la Terre, alors les rayons de S qui arrivent à Syène sont parallèles aux rayons qui arrivent à Alexandrie. L’angle entre les rayons du Soleil et le gnomon à Alexandrie est donc le même que l’angle formé par Syène, le centre de la Terre et Alexandrie (angles en rouge foncé sur le schéma).
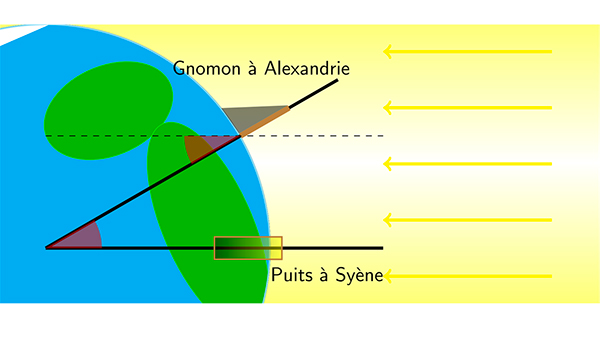
Sachant qu’il y a cinq mille stades entre Syène et Alexandrie, il en déduit par une règle de trois que la circonférence de la Terre est égale à (5 000 × 360) / 7, soit 250 000 stades.
On ne connaît malheureusement pas exactement la valeur du stade, qui de toutes façons variait d’un endroit à l’autre, mais on estime que deux cent cinquante mille stades font environ quarante mille kilomètres. Et puisque la circonférence d’un cercle vaut π fois son diamètre, on trouve un rayon pour la Terre de 6 500 km. On sait aujourd’hui que le rayon moyen de la Terre est de 6 371 km. Ératosthène n’était donc pas loin de la valeur exacte, en dépit des approximations qu’il a dû faire !
L’astuce de Christophe Colomb
Christophe Colomb (1451–1506) fut en son temps au cœur d’une controverse. La question ne portait pas sur la rotondité de la Terre (comme on peut parfois le lire), mais sur son diamètre. À l’époque, plusieurs estimations du diamètre de la Terre avaient été faites, et pour justifier son voyage et obtenir des fonds, il a choisi d’utiliser la plus basse. Tout le monde lui disait qu’il n’arriverait jamais à destination parce que la Terre est plus grande que ce qu’il supposait, pas parce qu’ils pensaient que la Terre est plate !

Décrocher la Lune
Une fois connu le diamètre de la Terre, il est possible de déterminer le diamètre de l’orbite de la Lune ! En –270, Aristarque avait observé qu’une éclipse lunaire dure au plus trois heures et que le diamètre apparent de la Lune est de 0,5°.
Une éclipse lunaire se produit lorsque la Lune (L) passe dans l’ombre de la Terre. Si le Soleil est « suffisamment éloigné », les rayons qui arrivent sur Terre sont tous parallèles les uns aux autres. Le diamètre de l’ombre de la Terre est alors égal au rayon de la Terre.
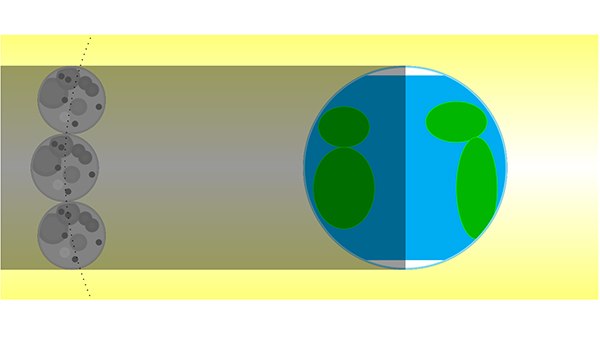
Puisqu’il faut trois heures à la Lune pour parcourir un rayon terrestre, on en déduit par une règle de trois qu’elle parcourt (27 j × 24 h) / 3 h = 216 diamètres terrestres par orbite. En d’autres termes, la circonférence de l’orbite de la Lune est de 216 diamètres terrestres. Le périmètre d’un cercle est égal à π fois son diamètre. Le diamètre de l’orbite de L représente donc environ 70 diamètres terrestres (ce qui fera remarquer que le schéma est loin d’être à l’échelle !).
Aristarque a ainsi trouvé que la Lune se situe à 450 000 km de la Terre alors que la valeur exacte est de 380 000 km. Aristarque avait donc obtenu le bon ordre de grandeur, en dépit des approximations qu’il a utilisées, notamment :
• son estimation du rayon de T n’était pas exacte ;
• l’ombre de la Terre est un cône, pas un cylindre.
La méthode de calcul appliquée à Mars
Le diamètre apparent θ du plus grand satellite de Mars, Phobos, est de θz = 0,22° lorsque la planète Rouge est au zénith, mais seulement θz = 0,15° lorsqu’elle est sur l’horizon, soit un écart de 32 %. Si une civilisation évoluée était apparue sur Mars (M), les savants auraient sûrement remarqué un tel écart et auraient pu s’en servir pour trouver la distance qui les sépare de Phobos (P).
Notons RM le rayon de Mars, RP celui de Phobos, RO celui de l’orbite de P, dh la distance de l’observateur (martien) à P lorsque le satellite est sur l’horizon, et dz cette distance lorsque P est au zénith. Le diamètre apparent θ de Phobos est l’angle sous lequel il est vu par l’observateur. Ainsi, lorsque P est à une distance d de l’observateur, on a tan(θ) = RP / d.
Lorsque Phobos est au zénith, la distance entre l’observateur et P est simplement la différence entre le rayon de Mars et le rayon de l’orbite de son satellite, soit dz = RO – RM. Lorsque Phobos est sur l’horizon, le théorème de Pythagore dans le triangle formé par l’observateur, P et le centre de M donne
Puisque le diamètre apparent de P est « très petit », on peut utiliser l’approximation tan(θ) ≃ θ. Le rapport entre le diamètre apparent au zénith et le diamètre apparent à l’horizon s’écrit alors :
En notant x = RM / RO, on se retrouve avec l’équation suivante :
que l’on peut résoudre numériquement. On trace la courbe d’équation y = 1,46 (en rouge) et celle d’équation (en bleu).
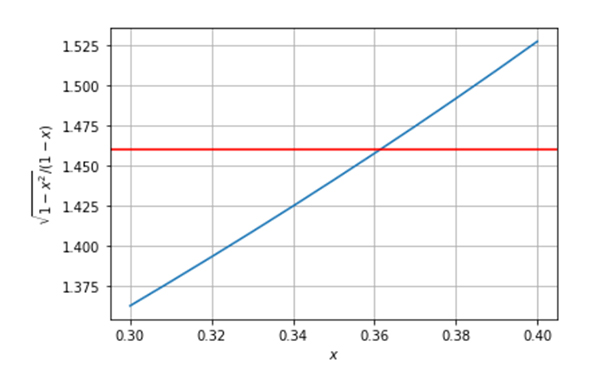
En repérant l’endroit où les deux courbes se croisent, on trouve ainsi RM ≃ 0,36 RO. En d’autres termes, le rayon de l’orbite de Phobos est 2,8 fois plus grand que le rayon de la planète Mars. Si les Martiens ont trouvé le rayon de Mars avec une méthode semblable à celle d’Ératosthène, alors ils savent que le rayon de l’orbite de P est d’environ 9 200 km.
Le Soleil… ou pas
Une fois connue la distance Terre–Lune, Aristarque s’est mis en tête de mesurer la distance Terre–Soleil. Pour ce faire, il a eu une idée plutôt astucieuse : lorsque la droite (TL) est perpendiculaire à la droite (TS), on voit « un peu plus » qu’un quartier de la Lune. Dit autrement, lorsqu’un observateur du côté nuit de la Terre voit très précisément un quartier de Lune, alors l’angle entre la Lune, la Terre et le Soleil est inférieur à 90°.
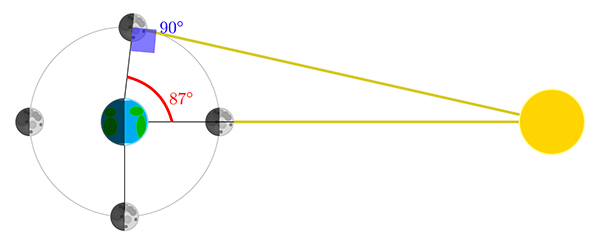
Il suffit alors de mesurer cet angle et d’utiliser un peu de trigonométrie pour en déduire la distance TS. Aristarque estime que cet angle vaut 87°. Au moment du quartier, on trouve, dans le triangle TLS :
D’après Aristarque, S est donc vingt fois plus éloigné de T que ne l’est L, ce qui correspond à une distance Terre–Soleil de neuf millions de kilomètres.
La méthode d’Aristarque était intéressante, mais son estimation était inexacte : l’angle entre le Soleil, la Terre et la Lune vaut en fait 89,85°. Mesurer cet angle n’est pas chose aisée : la surface de la Lune n’est pas lisse, donc le terminateur n’est pas un segment de droite, et le Soleil n’est pas visible dans le ciel au moment de la mesure. En outre, comme on prend le cosinus de l’angle, cette erreur de moins de 3° se traduit par une erreur de plus de cent millions de kilomètres ! Le Soleil est donc bien plus éloigné de la Terre que ne le pensait Aristarque.
Une fois qu’Aristarque avait calculé la distance TS, il s’est servi de cette information pour trouver le diamètre du Soleil. Sachant que notre satellite et notre astre ont le même diamètre apparent dans le ciel, et pensant que le second est vingt fois plus éloigné de nous que le premier, il a appliqué le théorème de Thalès pour en déduire que le Soleil est vingt fois plus grand que la Lune. Il s’est alors demandé pourquoi le Soleil tournerait autour de la Terre plutôt que le contraire, puisque le Soleil est plus grand. En somme, un peu d’observation et de géométrie lui ont permis de remettre en cause le modèle géocentrique.

Accéder aux planètes
C’est Copernic, vers 1543, qui a débloqué la clé pour mesurer la distance des planètes. Puisque toutes les planètes sont en orbite autour du Soleil, il suffit de mesurer l’angle θ sur la voûte céleste entre S et la planète étudiée. Pour une planète intérieure comme Vénus (V), l’angle θ est maximal lorsque l’angle formé par S, V et T est droit. On a alors sin(θ) = SV / ST.
.jpg)
Cependant, si l’on ne connaît pas la distance entre la Terre et le Soleil, cela ne nous donne qu’une partie de l’équation. Comme on ne sait pas encore déterminer cette distance, on introduit une nouvelle unité de mesure : l’unité astronomique (u.a.), qui vaut la distance moyenne entre la Terre et le Soleil. Même si l’on ne sait pas combien de kilomètres il y a dans une unité astronomique, on peut ainsi toujours exprimer les distances des planètes en u.a.
Le transit de Vénus
Au XVIIe siècle, Johannes Kepler a appliqué son modèle pour décrire les orbites planétaires à la Terre et a déterminé que si le Soleil n’était qu’à dix millions de kilomètres, comme le prédit le modèle d’Aristarque, alors on devrait voir des mouvements apparents du Soleil que l’on n’observe pas en pratique. Il en a déduit qu’Aristarque avait sous-estimé la distance TS.

Johannes Kepler (1571–1630).
Par la suite, de nombreux scientifiques ont tenté de mesurer la distance TS, avec des estimations qui allaient du simple au centuple ! Ce n’est qu’à partir du XVIIIe siècle que les estimations ont commencé à converger.
Un transit est le passage d’un astre ou d’une planète devant un autre corps céleste. Par exemple lorsque Vénus ou Mercure passe directement entre le Soleil et la Terre. On peut alors observer la planète qui obscurcit une partie du disque solaire.
Au tout début du XVIIe siècle, l’astronome Edmond Halley (1656–1742) avait été très impressionné par l’observation d’un transit de Mercure. Cet évènement l’a beaucoup fait réfléchir ; il a publié un article expliquant comment on peut utiliser le transit d’une planète pour déterminer la valeur de l’unité astronomique.
Pour le transit de Vénus de 1761, plusieurs expéditions ont été montées pour observer l’évènement depuis différents endroits sur Terre. Plus de deux cents astronomes ont observé le phénomène. C’était en quelque sorte la première grande collaboration scientifique internationale.
En fonction de l’endroit où on se trouve sur la Terre, Vénus ne transite pas devant la même portion du disque solaire. Le phénomène est alors plus ou moins long. En comparant la durée du transit d’un endroit à l’autre, on peut en déduire la valeur de l’unité astronomique !
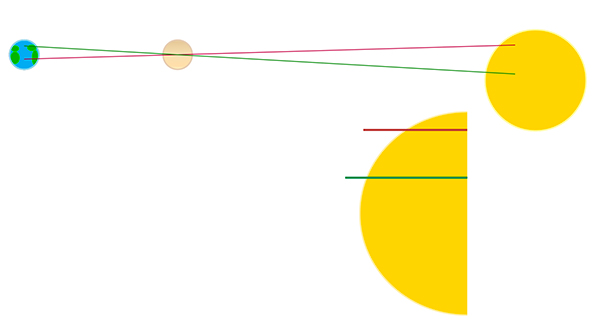
Depuis la Terre, on verra Vénus passer devant le disque solaire, mais tous les observateurs ne verront pas Vénus dans la même configuration par rapport au Soleil. Dans le schéma, l’astronome dans l’hémisphère sud verra Vénus passer le long du segment rouge, tandis que l’observateur de l’hémisphère nord verra Vénus emprunter le segment vert.
Suite au transit de 1761, Johann Franz Encke a trouvé une distance TS de 153 millions de kilomètres, très proche des 140 millions que l’on connaît aujourd’hui.

Johann Franz Encke (1791–1895).
Ces observations de 1761 n’ont pas été très probantes pour connaître la valeur de l’unité astronomique, car il y avait encore d’assez grandes erreurs de mesure. Elles ont cependant permis aux astronomes de s’entraîner pour le transit de Vénus de 1769. Surtout, l’évènement de 1761 marque le début de la convergence des différentes valeurs de la distance TS.
Dans les années suivantes, les différentes estimations se sont resserrées de plus en plus, jusqu’à tenir dans un mouchoir de poche. On a alors atteint un consensus scientifique sur la valeur de l’unité astronomique.
Connaissant la distance Terre–Soleil, on peut donc enfin déterminer précisément la distance de toutes les planètes à la Terre.
Aujourd’hui, on dispose de moyens technologiques plus sophistiqués pour mesurer la distance des objets dans le système solaire. Sur la Lune, on a placé des réflecteurs qui ont permis de constater que la Lune s’éloigne de 4 cm chaque année.
La distance du Soleil est mesurée très précisément par radar. Notre connaissance du système solaire s’en trouve renforcée !
Ce texte a remporté le Prix Tangente du meilleur article en 2021.
