Les échecs sont un jeu extrêmement subtil tant pour l’affrontement stratégique des deux joueurs que pour l’analyse mathématique des parties envisageables. Il est toutefois possible de s’adonner à une variante plus élémentaire, accessible même aux néophytes, et qui demeure un tantinet intéressante à partir du même matériel.
Pour les préparatifs : considérez un échiquier (vous pouvez prendre un damier plus grand) et orientez-le, c’est-à-dire mettez-vous d’accord avec votre adversaire pour distinguer la gauche de la droite, le bas du haut (voir notre dossier « L’orientation », Tangente 206, 2022). Posez ensuite une dame sur une case ; le match peut démarrer !
Il y a deux règles : les joueurs déplacent la dame à tour de rôle, du nombre de cases qu’ils souhaitent mais seulement vers la gauche, vers le bas, ou en diagonale vers le bas-gauche ; le joueur qui ne peut plus avancer la pièce (c’est-à-dire si c’est son tour de jouer et si la pièce se trouve déjà dans le coin bas gauche) a perdu.
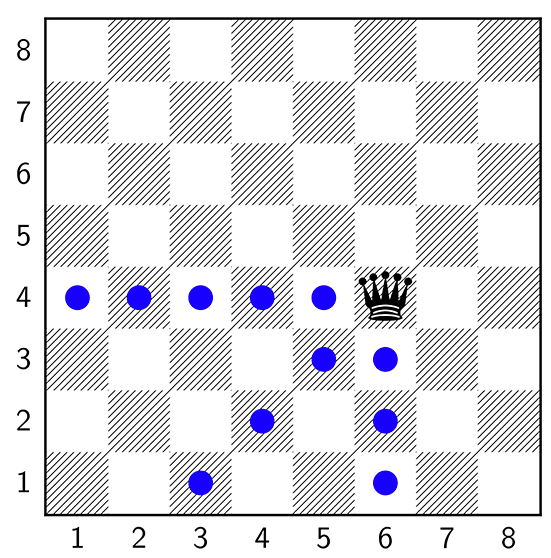
Exemple de toutes les positions accessibles depuis une case donnée.
Ce jeu est plus facile que les échecs, mais peut toutefois procurer quelques satisfactions et attiser la curiosité tant des joueurs que des mathématiciens. Nous vous encourageons à l’expérimenter avant de poursuivre votre lecture.
Positions gagnantes et positions perdantes
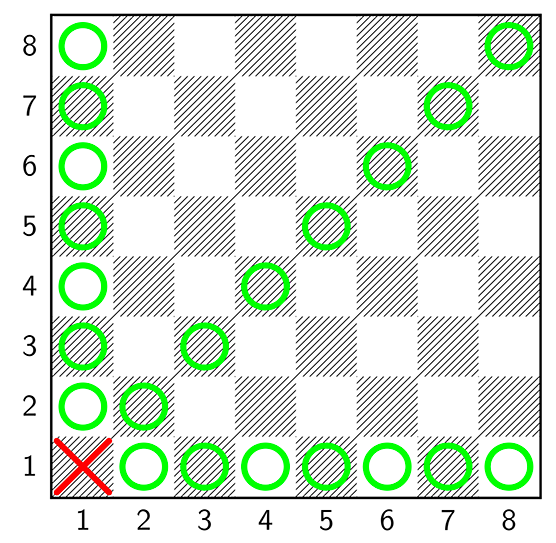
Pour analyser le jeu, remarquons déjà que si la dame est initialement dans le coin bas-gauche, le premier joueur ne peut pas la déplacer en respectant la règle, donc a perdu ; en revanche, si la dame se trouve en n’importe quelle autre case de la première colonne, de la première ligne ou de la diagonale, alors le premier joueur dispose d’une stratégie gagnante évidente : il déplace la dame tout au bout de cette ligne/colonne/diagonale vers le coin bas-gauche pour bloquer définitivement son adversaire.
Positions gagnantes et perdantes après la première étape de raisonnement
(croix rouge : position perdante, rond vert : position gagnante).
Imaginons maintenant que la dame soit initialement sur la troisième colonne (en partant de la gauche) et deuxième ligne (en partant du bas), position que l’on note (3, 2). Le joueur peut la déplacer :
• soit vers la gauche : aux positions (2, 2), déplacement d’une case, ou (1, 2), déplacement de deux cases ;
• soit vers le bas : à la position (3, 1) ;
• soit en diagonale : à la position (2, 1).
Il ne peut immédiatement amener la dame dans le coin bas-gauche, et, quel que soit son choix de déplacement, elle se trouve désormais sur la première ligne, sur la première colonne ou sur la diagonale issue du coin bas-gauche. Le second joueur pourra donc sans difficulté la mettre au coin et emporter la partie. Cette position (3, 2) est donc perdante pour le premier joueur si son adversaire joue bien : quoi qu’il fasse, le second joueur dispose d’une stratégie gagnante. Vous pouvez poursuivre l’analyse à la main et vérifier par exemple que la position (6, 4) est, elle aussi, perdante pour le joueur qui entame la partie.
À ce stade, on a donc vu qu’il existait deux types de position : celles où le premier joueur dispose d’une stratégie gagnante à coup sûr et celles où sa position est perdante. L’enjeu est donc de cataloguer toutes les positions au regard de ce critère. Plus précisément, une case est perdante si c’est le coin en bas à gauche, ou si tous les mouvements depuis cette case amènent l’adversaire vers une position gagnante ; une case est gagnante s’il existe un mouvement qui amène l’adversaire vers une position perdante. Cette définition est délicate à cause de sa structure récursive : on a l’impression, si on lit trop vite, que celle-ci n’est pas correcte et qu’elle « boucle ». Ce n’est pas le cas : elle permet de déterminer (progressivement et, il faut l’admettre, laborieusement) le statut de toutes les cases de l’échiquier. On place une croix rouge sur les positions perdantes (au départ, seul le coin bas gauche), puis des ronds verts sur toutes les cases qui permettent d’aller vers une croix rouge, puis une croix rouge sur les cases qui ne mènent qu’à des ronds verts, et ainsi de suite. On obtient, après quelques étapes, le résultat de la figure ci-dessous.
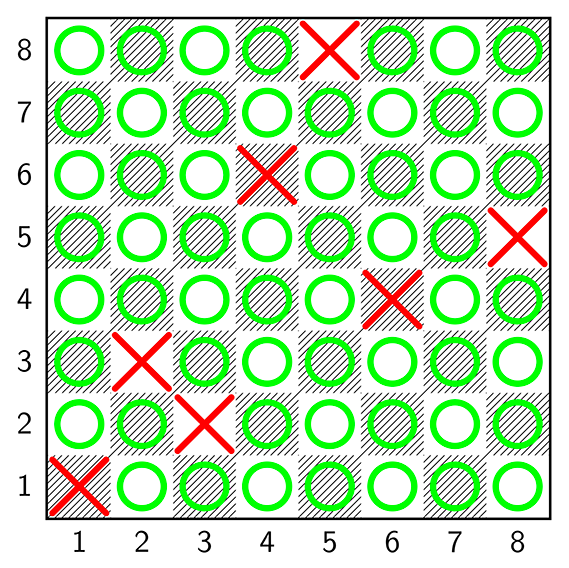
Analyse complète de toutes les positions sur l’échiquier.
De manière tout à fait logique, il n’y a jamais deux positions perdantes sur la même ligne, la même colonne ou la même « diagonale ». C’est un joli exercice d’appropriation de la définition que de montrer cette propriété !
La généralisation de Sprague et Grundy
Revenons au jeu après avoir obtenu ce diagramme et explicitons une « bonne » façon de jouer en partant d’une case marquée d’un rond vert ; la stratégie gagnante consiste à déplacer la dame vers une case marquée d’une croix rouge (c’est toujours possible d’après la définition). Ensuite votre adversaire, s’il n’a pas déjà perdu, va nécessairement ramener la dame vers un rond vert : là encore, son choix est contraint par la définition ! Poursuivant ainsi, vous jouerez toujours depuis un rond vert et votre adversaire depuis une croix rouge. Comme la position de blocage (coin bas-gauche) est marquée d’une croix rouge, seul votre adversaire pourra s’y trouver et vous ne pouvez pas perdre. Il suffit de remarquer qu’il y aura forcément un perdant (impossible d’avoir une partie nulle ou infinie avec ces règles) pour conclure que vous allez gagner.
Cette façon d’analyser les jeux, de distinguer et déterminer progressivement les configurations « gagnantes » et « perdantes », n’est pas propre à ce jeu. Elle a été étendue dans les années 1930 par l’Allemand Roland Percival Sprague (1894‒1967) et le Britannique Patrick Michael Grundy (1917‒1959) à d’autres jeux vérifiant quelques hypothèses simples : les deux joueurs qui jouent à tour de rôle ne peuvent faire partie nulle ou poursuivre indéfiniment une partie et il y a une forme d’« impartialité » entre les joueurs (au sens que si les deux joueurs se retrouvaient dans la même configuration de jeu, ils auraient les mêmes possibilités de jouer).
Ce cadre théorique exclut bon nombre de distractions de notre quotidien, comme les échecs ou le go ; en revanche, on en retrouve d’autres, comme le jeu des allumettes (ou jeu de nim), le sprouts (ou jeu des pousses) ou même le retire un carré, qui amuse certains mathématiciens : partant d’un nombre entier, les joueurs soustraient à tour de rôle le carré d’un entier. Par exemple, on peut passer de 37 à :
36 = 37 – 12 ; 33 = 37 – 22 ;
28 = 37 – 32 ; 21 = 37 – 42 ;
12 = 37 – 52 ; 1 = 37 – 62.
Celui qui arrive à 0 a perdu.
Il y a toutefois un petit bonus mathématique dans le jeu de la dame sur l’échiquier : l’ensemble des positions gagnantes est non seulement déterminé par la méthode de Sprague‒Grundy (indiquée plus haut), mais aussi complètement élucidé par une formule mathématique explicite !
Le mathématicien néerlandais Willem Abraham Wythoff (1865‒1939) a ainsi obtenu dès 1907 les coordonnées de toutes les positions perdantes et, petite surprise, celles-ci s’expriment simplement à partir du nombre d’or (voir notre dossier dans Tangente 203, 2022) et d’un paramètre entier : pour chaque valeur du paramètre, on obtient une position perdante et chaque position perdante correspond à une valeur du paramètre. Il est toujours stupéfiant de voir apparaître ainsi des mathématiques derrière une situation anodine !