La notion a le parfum oublié des vieux livres de géométrie, En tout cas, elle figurait en bonne place dans les manuels de seconde des années soixante, où le titre « Puissance d’un point par rapport à un cercle » était un chapitre à part entière, avec ses applications : problèmes de construction, conditions pour que des points soient situés sur un même cercle, recherche de lieux géométriques.
Un concept un peu oublié
On définit la puissance d’un point P du plan par rapport à une conique (K) comme le minimum du produit des mesures algébriques
et
, M et N étant les intersections de (K) avec une droite quelconque passant par P. C’est au mathématicien suisse Jakob Steiner (1796‒1863) que revient la définition actuelle de la puissance d’un point par rapport à un cercle, considéré comme une conique particulière.
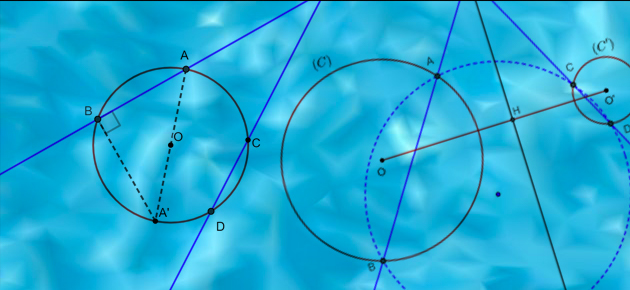
Parler de puissance d’un point P par rapport à un cercle (C) revient donc à considérer une droite passant par P qui coupe (C) en A et B ; la puissance est alors exactement le produit car, dans le cas du cercle, résultat remarquable, ce produit est constant quelle que soit cette sécante. ... Lire la suite
