
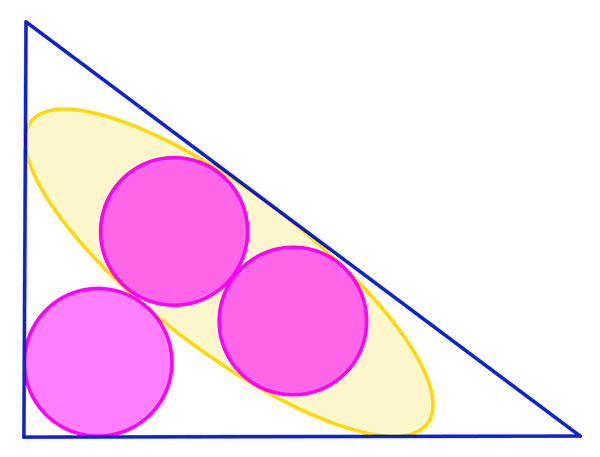
Dans le premier problème, proposé par Sawa Masahoshi, une ellipse est inscrite dans un triangle rectangle et son grand axe est parallèle à l’hypoténuse. Deux cercles tangents de même rayon sont inscrits dans l’ellipse. Un troisième cercle, de même rayon que les deux premiers, est tangent à la fois à l’ellipse et aux deux autres côtés du triangle.
Le but est d’exprimer le rayon commun des trois cercles en fonction des côtés du triangle.
La seconde énigme pourrait faire penser au plus célèbre des sangaku. On considère deux cercles tangents et une tangente commune à ces deux cercles. Au lieu d’inscrire un cercle dans la petite région délimitée par ces trois objets, on propose d’y inscrire… un carré, de façon qu’un sommet soit en contact avec la tangente, et deux autres avec les deux cercles.
L’auteur de ce sangaku, Jihei Morikawa, demande d’exprimer le côté du carré en fonction des rayons des deux cercles.

Le point commun à ces deux questions ? Aucune réponse ne figurait sur les tablettes originales et elles n’ont été résolues que… très récemment ! Pour la première, la réponse, difficilement reproductible ici, a été apportée en 2018 par Hiroshi Kinoshita dans le Sangaku Journal of mathematics.
Quant ... Lire la suite gratuitement
