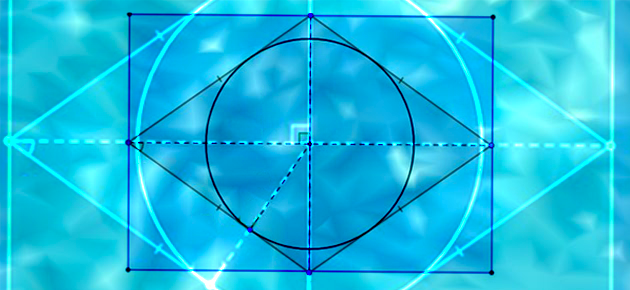
Un losange ne peut être défini par la seule donnée de la longueur d’un côté, soit a ; il nous faut également la valeur de l’angle entre deux côtés successifs, soit α. Les deux losanges ci-contre ont des côtés de même longueur a, mais des angles au sommet différents. Ce sont donc des objets mathématiques différents, même si leurs côtés sont de même longueur. Ont-ils la même aire ?
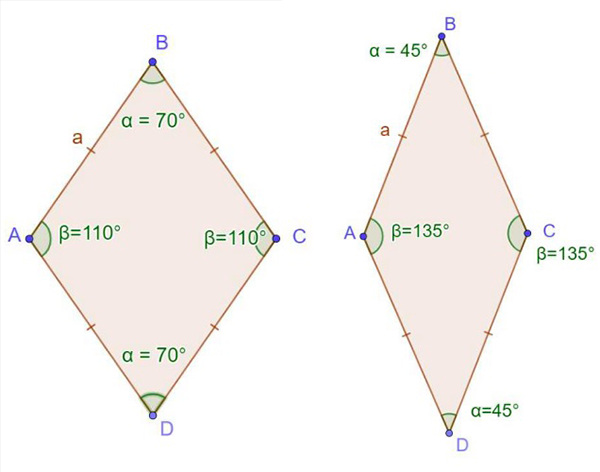
Deux losanges. Lequel est « plus grand » que l’autre ?
Un calcul élémentaire
L’une des propriétés remarquables des losanges est que leurs diagonales sont perpendiculaires et qu’elles se coupent en leurs milieux. Le losange est donc formé de quatre triangles rectangles identiques dont il est aisé de calculer l’aire.
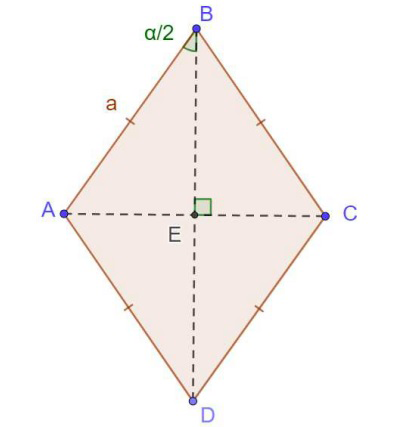
Les diagonales du losange se coupent en leurs milieux.
L’aire du triangle AEB est avec AE = a sin(α/2) et EB = a cos(α/2).
On obtient donc, comme valeur de l’aire du triangle, soit encore
en utilisant l’expression sin 2α = 2 sin α cos α, valable pour tout réel α.
L’aire du losange devient a2 sin α ; elle est calculable dès ... Lire la suite
