
Cryptarithmes
Comme pour tout cryptarithme, il s’agit de reconstituer cette addition où deux lettres représentent deux chiffres différents, et où aucun nombre ne commence par zéro.
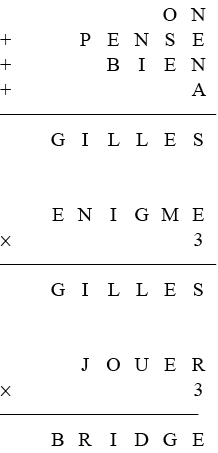
Les amies espiègles
Estelle et Chloé sont fans d’énigmes mathématiques.
1. Un jour, Estelle envoie à Chloé le message suivant : « Voici cinq nombres : 346, 905, 376, 845 et 305. Mon numéro fétiche est un nombre à trois chiffres et chacun des cinq nombres donnés comporte un et seul chiffre qui est positionné à la bonne place de mon numéro fétiche. »
Quel est le numéro fétiche d’Estelle ?
2. Quelques jours plus tard, Chloé envoie un mot à Estelle : « J’espère que tu pourras venir à mon anniversaire. Voici huit nombres : 4 358, 1 026, 7 944, 3 817, 4 659, 2 751, 8 903 et 5 227. Le code d’entrée de mon immeuble a été changé, c’est un nombre à quatre chiffres et chacun des huit nombres donnés comporte un et un seul chiffre qui est positionné à la bonne place du code d’entrée de mon immeuble. »
Quel est le code d’entrée de l’immeuble de Chloé ?
Principe des tiroirs : pensez à la tangente !
Essayez de résoudre cette petite énigme combinatoire d’apparence inoffensive : montrer que, dans tout ensemble E de cinq nombres réels, il en existe deux, a et b, tels que .
Les techniques usuelles de l’arithmétique, de la combinatoire ou encore de l’analyse ne vous permettront pas de résoudre immédiatement cette innocente question. Dès lors, pensez à un changement de variable !
Le paradoxe de Bertrand
On dispose de trois boîtes identiques. La première contient deux billes vertes, la deuxième une bille verte et une bille rouge, la troisième deux billes rouges. On tire au hasard l’une des boîtes (avec égales probabilités) et dans cette boîte on prend au hasard l’une des deux billes (aussi avec égales probabilités).
1. Si l’on constate que la bille tirée est rouge, quelle est la probabilité que l’autre bille dans la même boîte soit rouge ?
On a cette fois n + 1 boîtes contenant chacune n billes (avec n ≥ 2). Pour 0 ≤ k ≤ n, la boîte numéro k contient k billes rouges et n − k billes vertes. On tire de même l’une des boîtes au hasard, puis l’une des billes dans cette boîte (chaque fois de façon équiprobable).
2. Constatant que la bille tirée est rouge, si l’on tire au hasard une deuxième bille dans la même boîte (sans y avoir replacé la première bille tirée), quelle est la probabilité qu’elle soit rouge ?
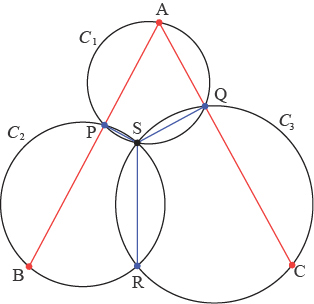
Trois points alignés ?
Les trois cercles C1, C2, C3 sont concourants en S. Les cercles C1, C2 se recoupent en P, les cercles C1, C3 se recoupent en Q et les cercles C2, C3 se recoupent en R. Le point A (non confondu avec P ou Q) est pris sur le cercle C1. La droite (AP) recoupe le cercle C2 en B et la droite (AQ) recoupe le cercle C3 en C.
Les points B, R, C semblent alignés. Est-ce vrai ?
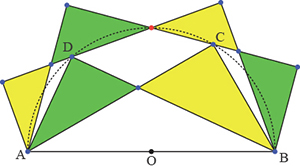
Trois lopins de terre
Alice et Bob disposent chacun de trois lopins de terre en forme de triangle rectangle. Les points C et D sont sur le demi-cercle de diamètre AB. Sur les segments [AD], [DB], [AC] et [CB], on a disposé des triangles isocèles rectangles. L’aire totale du domaine d’Alice (en jaune) semble égale à celle du domaine de Bob (en vert).
Si c’est le cas, prouvez-le ! Si ce n’est pas le cas, prouvez-le !
Trois vases
Alice propose à Bob le jeu suivant : elle dispose trois vases, que l’on nommera A, B et C. Dans le vase A, elle place treize jetons ; dans le vase B, elle place quinze jetons et dans le vase C, elle en place dix-sept. À chaque étape, Bob choisit deux vases où il reste au moins un pion, il enlève un pion dans chacun de ces deux vases et il les place dans le troisième vase. L’objectif est d’obtenir deux vases vides, tous les pions se trouvant donc dans un seul vase.
Bob pourra-t-il atteindre cet objecti ? Si oui, en combien d’étapes au minimum ?
Problèmes de voisinage
On considère des cases alignées et numérotées de 1 à n.
1. Deux cases i et j sont voisines si | i – j | = 1. On veut colorier ces cases en noir (N) ou blanc (B) de sorte que chaque case N ait exactement deux cases voisines B et que chaque case B ait exactement une case voisine N. Pour quelles valeurs de n est-ce possible ?
2. On étend la notion de « voisinage » : deux cases i et j sont maintenant « voisines » si | i – j | ≤ 2. On veut colorier ces cases en noir (N) ou blanc (B) de sorte que chaque case N ait deux ou quatre cases voisines B et que chaque case B ait une ou trois cases voisines N. Pour quelles valeurs de n cela est-il possible ?
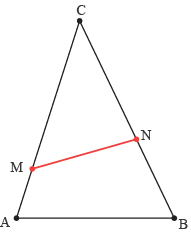
Bipartition d’un triangle en deux régions de même aire
Sur le côté [AC] du triangle ABC on place un point M, « plus proche » de A que de C. Proposer plusieurs méthodes pour obtenir le point N sur le côté [BC] tel que le segment [MN] partage le triangle ABC en deux régions de même aire.
Vous trouverez les solutions des problèmes de cette page, ainsi que les témoignages complets des amis de Gilles, dans la version numérique de ce numéro sur tangente-mag.com.
