Pour construire un graphe divisoriel, commencez par fixer un entier n, appelé l’indice du graphe. Les sommets du graphe sont alors les entiers 1, 2... jusqu’à n. Une arête relie deux entiers distincts dans ce graphe si le plus grand des deux est un multiple du plus petit (ou de manière équivalente, si le plus petit divise le plus grand). Par exemple, dans le graphe divisoriel d’indice n = 6 (dont un dessin est ci-dessous), on dénombre 6 sommets ; le sommet 1 est relié à tous les autres, le sommet 2 à 1, 4 et 6, le sommet 3 seulement à 1 et 6 et l’on a ainsi toutes les arêtes (les arêtes qui relient 4 à 1, 4 à 2, 5 à 1, 6 à 1, 6 à 3 sont déjà tracées).
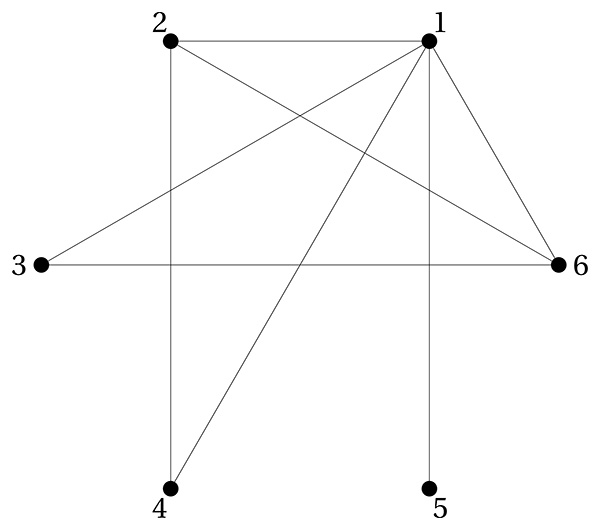
Graphe divisoriel d’indice 6.
On constate immédiatement certaines propriétés : le sommet 1 est relié à tous les autres sommets ; un sommet correspondant à un nombre premier n’est relié qu’à ses multiples et à 1, donc assez peu de sommets ; à l’opposé, un entier avec beaucoup de diviseurs est relié à de nombreux sommets.
Ces remarques peuvent donner une idée de la structure ... Lire la suite
