
Le mathématicien allemand Georg Cantor voit le jour en Russie de parents danois. Il vit à partir de 1856 à Francfort. Son père, protestant d’origine juive, et sa mère, catholique, lui communiquent sa passion pour la théologie médiévale, probablement à l’origine de ses arguments compliqués sur la continuité et l’infini. Il étudie à Zurich, puis en Allemagne, à Berlin. Il y suit les cours de Weierstrass, le père de l’analyse moderne, de Kummer et de Kronecker, tous deux grands spécialistes de la théorie des nombres. Il complète sa formation par des études de physique et de philosophie.
Après un semestre à l’université de Göttingen, il soutient en 1867 sa thèse de doctorat, sans doute l’un des derniers textes mathématiques écrits en latin : In re mathematica ars propendi pluris facienda est quam solvendi (« En mathématiques, l’art de calculer est plus important que résoudre »). Il obtient en 1869 un poste de professeur à l’université de Halle, qu’il ne quitte qu’en 1905 pour ne plus enseigner.
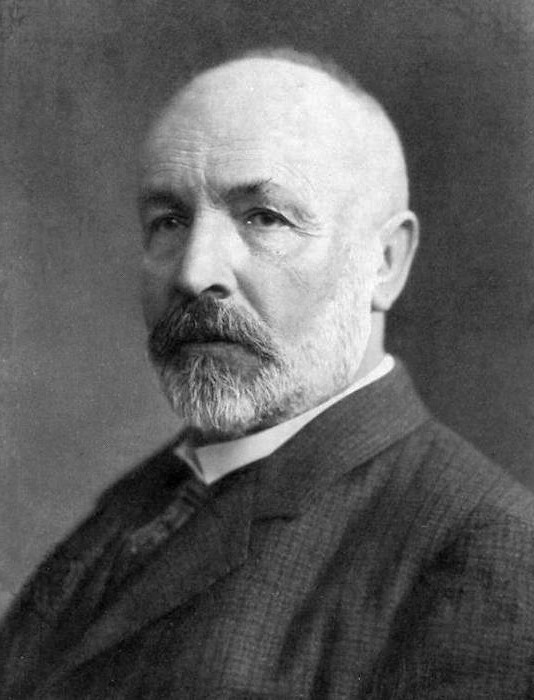
Georg Ferdinand Ludwig Philipp Cantor (1845—1918).

La place du marché de Halle entre 1890 et 1905 (lithographie coloriée).

L’université de Halle vers 1880.
La genèse de la théorie des ensembles
Les premiers intérêts mathématiques de Cantor concernent la théorie des nombres. Mais rapidement son collègue Eduard Heine, de vingt-quatre ans son aîné, l’encourage à étudier la théorie des séries de Fourier. Cantor démontre que si une fonction périodique est égale en tout point à la somme d’une série trigonométrique, celle-ci est unique. Il étend cette unicité au cas où la convergence se produit partout sauf en un nombre fini de points. C’est ainsi que son intérêt se porte sur des ensembles de points et qu’il commence à ébaucher la théorie des ensembles avec un point de vue topologique, et des réflexions sur les ensembles infinis de points.
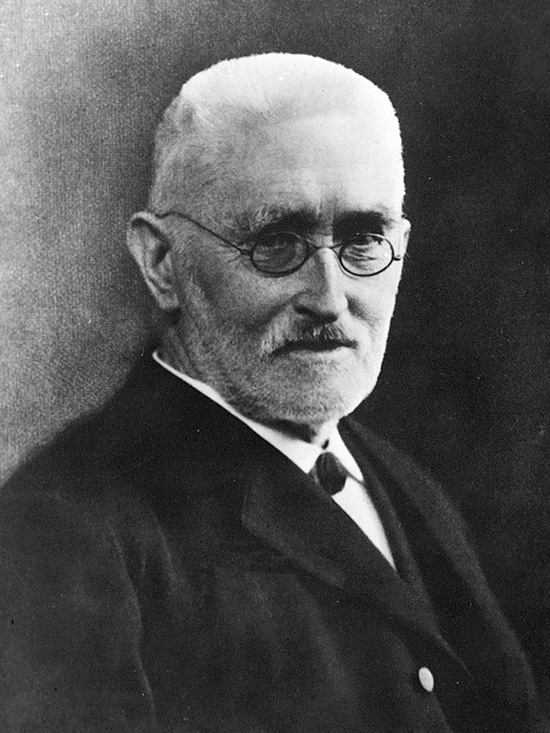
Julius Wilhelm Richard Dedekind (1831—1916).
Lors d’un voyage en amoureux avec sa femme à Interlaken, en Suisse, en 1872, Cantor rencontre le mathématicien allemand Richard Dedekind. Les deux mathématiciens échangent alors leurs idées sur les notions d’ensembles infinis.
À la fin de l’année suivante, Cantor constate (en utilisant la terminologie actuelle) que l’on peut définir une bijection entre l’ensemble des nombres rationnels et celui des entiers positifs, montrant ainsi que l’on peut mettre l’ensemble de toutes les fractions sous la forme d’une suite. Dedekind prouve que l’ensemble des nombres algébriques, c’est-à-dire des nombres qui sont racines d’un polynôme à coefficients entiers, est lui aussi dénombrable, c’est-à-dire en bijection avec l’ensemble ℕ des entiers naturels. Cantor en déduit que si l’on démontrait que l’ensemble ℝ des nombres réels n’est pas équipotent à ℕ, on montrerait qu’il existe des nombres transcendants, c’est-à-dire non algébriques.
Ce résultat avait été montré par Joseph Liouville en 1844 en exhibant explicitement de tels nombres. C’est une démarche tout à fait nouvelle que pressent Cantor : justifier une existence par une comparaison de cardinaux et sans exhiber un seul élément. De plus, ceci montrerait qu’il existe « plusieurs infinis » ; qui sait, une infinité d’infinis !
Le mathématicien allemand s’attache à démontrer que ℝ n’est pas dénombrable. Il parvient rapidement à ce résultat, qu’il présente dans un article signé l’avant-veille de Noël 1873 ; il le fait par un raisonnement par l’absurde basé sur la construction de segments emboîtés. Il termine son texte en remarquant que l’on peut déduire de ce résultat, exposé ici en termes modernes, que si un une famille finie ou dénombrable de réels forme un système libre sur l’ensemble des rationnels, alors tout intervalle de ℝ contient une infinité de termes qui ne s’expriment pas comme une combinaison linéaire à coefficients rationnels des éléments de cette famille. En d’autres termes, ℝ, considéré comme un espace vectoriel sur ℚ, ne possède aucune base ni finie, ni dénombrable.
L’approche de Cantor imbrique des notions ensemblistes et topologiques. Ceci explique sa stupéfaction lorsque, en 1877, il envoie à Richard Dedekind sa preuve de l’existence d’une bijection entre ℝ2 et ℝ. Ainsi, il y aurait autant de points sur une droite que dans un plan, alors que la première n’est qu’une partie infime du second ! Ce résultat lui paraît tellement étonnant qu’il ajoute : « Tant que vous ne m’aurez pas approuvé, je ne puis que dire je le vois mais je ne le crois pas » (en français dans le texte original). Dedekind, d’abord incrédule, réagit cependant rapidement en affirmant qu’une telle fonction n’est certainement pas continue. En fait, il aurait dû dire « n’est pas un homéomorphisme ». La fonction remplissant un carré, proposée par Giuseppe Peano en 1890, est en effet continue !
Bientôt cependant, Cantor est l’objet de dépressions nerveuses intenses qui le conduisent à une première hospitalisation en 1884.
Les cardinaux transfinis
Cantor reprend cependant ses travaux et expose en 1891 une nouvelle preuve beaucoup plus simple du fait que ℝ n’est pas dénombrable. Sa démonstration n’est pas exactement ce que l’on appelle de nos jours la diagonale de Cantor mais elle possède en outre l’avantage de montrer que, pour tout ensemble, il n’existe aucune bijection entre celui-ci et l’ensemble de ses parties ; ceci est connu sous le nom de théorème de Cantor. Ainsi, le cardinal de l’ensemble ℘ (E) des parties de E est strictement plus grand que celui de l’ensemble E lui-même. Le rêve de Cantor se réalise : il existe une infinité d’infinis, il n’existe pas de « plus grand » cardinal.
Mais alors, qu’en est-il de « l’ensemble de tous les ensembles » ? Il devrait tous les contenir. Cantor entrevoit sans doute le paradoxe qui pourrait transformer le rêve en cauchemar et mettre à mal la théorie des cardinaux transfinis… et même celle des ensembles. Il achève son article en expliquant que les cardinaux infinis représentent l’unique et nécessaire généralisation des cardinaux finis et il affirme qu’ils ont la même réalité et certitude que ceux-ci. Il conclut en estimant qu’il appartient à l’avenir de mettre en valeur ce domaine.
Sur les fondements de la théorie des ensembles transfinis
L’ouvrage de Cantor est le véritable fondement de la théorie des ensembles. La traduction de Francisque Marotte a été approuvée par l’auteur, qui maîtrisait bien notre langue. Le terme même d’« ensemble », traduction de l’allemand Menge, est introduit ici. « Nous appelons ensemble toute réunion M d’objets de notre conception m, déterminés et bien distincts, et que nous nommerons éléments de M. »

Cantor définit alors la notion de puissance (Mächtigkeit) ou nombre cardinal (Cardinalzahl) de M comme étant « la notion générale que nous déduisons de M à l’aide de notre faculté de penser, en faisant abstraction de la nature des différents éléments m et de leur ordre ». Rassurez-vous, c’est plus clair par la suite ! Cantor dit « que deux ensembles sont équivalents [nous disons de nos jours équipotents] […] lorsqu’il est possible de les associer, de telle sorte qu’à chaque élément de l’un d’eux corresponde un et un seul élément du deuxième » ; ceci signifie qu’il existe une bijection entre les deux. Il poursuit en affirmant qu’« il est d’importance capitale que deux ensembles M et N ont alors le même nombre cardinal lorsqu’ils sont équivalents. »
Il explique alors qu’un cardinal a de l’ensemble M est plus grand (strictement) que celui b de N si :
Il n’y a aucune partie de M qui soit équivalente à N ;
Il y a une partie N1 de N qui soit équivalente à M.
Ceci correspond à dire qu’il existe une injection de M dans N mais aucune bijection entre les deux.
Cantor définit la somme et le produit de deux cardinaux comme le cardinal de la réunion disjointe des ensembles associés et comme le cardinal du produit cartésien.
Plus loin, il nomme ℵ0 (« aleph zéro ») le cardinal de l’ensemble des entiers positifs et montre que c’est le plus petit cardinal transfini, puis il caractérise les cardinaux transfinis come ceux vérifiant l’égalité a + 1 = a (en adjoignant un élément à un ensemble infini, on obtient un ensemble équipotent). Par exemple, l’ensemble ℕ est en bijection avec celui des entiers strictement positifs grâce à l’application qui, à n, associe n + 1.
En 1895, il rédige Beiträge zur Begründung der transfiniten Mengenlehre ; ce texte est aussitôt traduit dans notre langue (et relu par l’auteur) par le mathématicien Francisque Marotte (1873‒1945) avec le titre Sur les fondements de la théorie des ensembles transfinis. Cantor construit méthodiquement la théorie des cardinaux transfinis (voir encadrés). La principale pièce manquante au puzzle est le théorème de Cantor‒Bernstein, qui prouve l’antisymétrie de la relation d’ordre sur les cardinaux. Ce résultat sera démontré par Richard Dedekind, qui ne publie pas sa preuve, par Felix Bernstein (1878‒1956), un jeune étudiant de Cantor, et par Ernst Schröder (1841‒1902).

L’infini, d’Aristote à Cantor
Cantor a transformé la vision du concept d’infini dans la société occidentale. Cette notion est apparue en mathématiques dès Euclide, lorsqu’il montre qu’il existe une infinité de nombres premiers. Le mathématicien grec de l’Antiquité exprime ainsi dans la proposition 20 du livre IX : « Les nombres premiers sont plus nombreux que n’importe quelle multitude de nombres premiers proposée. »
On parle alors d’infini potentiel, c’est-à-dire que, quel que soit l’ensemble fini considéré, on peut toujours trouver un élément qui ne lui appartient pas. Cette doctrine avait été forgée philosophiquement par Aristote, qui refusait que l’on considère l’infini comme une totalité. Il faut dire que les nombreux paradoxes s’attachant à cette notion ne pouvaient que conforter cette idée… Descartes comme Spinoza partageaient également cette vision des choses mais pour ces deux philosophes, seul Dieu, parfait et omnipotent, pouvait s’identifier à un infini absolu.
Aussi, Georg Cantor rompt totalement avec ses prédécesseurs dans son étude des ensembles infinis et « change de paradigme », comme dirait l’épistémologue suisse Thomas Kuhn. Il introduit différents infinis et les considère comme des réalités mathématiques ; il les manie comme des totalités : on parle d’infini en acte.
Comment le mathématicien allemand a-t-il pu franchir cet « obstacle épistémologique », pour reprendre le vocabulaire de Gaston Bachelard ? Est-ce sa grande spiritualité qui lui a permis de mettre un concept mathématique à la place du Dieu de Descartes et de Spinoza ? Est-ce plutôt son parcours de crête aux confins des mathématiques de haut niveau et d’un certain degré de folie ? Peu importe. Pour reprendre la métaphore de David Hilbert, il nous a ouvert un paradis mathématique d’où nous ne sortirons plus.
Une fin de vie difficile
Le travail de Cantor est très contesté. Ses idées sont révolutionnaires pour l’époque. Le premier opposant est Leopold Kronecker, mais il n’est pas le seul : Henri Poincaré, Felix Klein et Hermann Weyl le critiquent également ; ce dernier qualifie ce travail de « brouillard dans le brouillard ». L’apparition de paradoxes, à partir de 1897, n’arrange rien et la réaction prend alors un tour passionnel, à tel point que les notions les plus courantes et les plus fécondes, les types d’arguments les plus simples et les plus importants des mathématiques, sont menacés d’interdit !

Leopold Kronecker (1823—1891).
L’année 1899 marque la fin de la période créatrice de Cantor. Il passe une partie de cette année, tragique pour lui, à la Nervenklinik, l’hôpital psychiatrique de Halle. Bientôt, ses dépressions nerveuses se font de plus en plus fréquentes et les séjours à la Nervenklinik de plus en plus longs.
Il meurt le 6 janvier 1918.

Nervenklinik, l’hôpital psychiatrique de Halle.
Malgré ces difficultés, l’importance du fondement des mathématiques que donne la théorie de Cantor séduit certains, comme Giuseppe Peano, Adolf Hurwitz et Jacques Hadamard, qui en expose des applications dès 1897. C’est cependant David Hilbert qui lui rendra le plus bel hommage, en affirmant : « Personne ne devrait pouvoir nous chasser du paradis que Cantor a créé pour nous. »

David Hilbert (1862—1943).
Cantor‒Bernstein : le chaînon manquant
Dans son ouvrage Sur les fondements de la théorie des ensembles transfinis, Cantor cherche à attribuer à chaque ensemble, fini ou infini, un cardinal, notion généralisant le nombre d’éléments pour un ensemble fini. Puis il souhaite définir un ordre total sur ces cardinaux. La difficulté est qu’il n’est plus possible de « compter » les éléments ! Penchons-nous d’abord sur les ensemble finis et exhibons des propriétés pouvant se généraliser pour les ensembles infinis.
Deux ensembles ont « le même nombre d’éléments » si l’on peut trouver une bijection entre les deux ; le cardinal de l’un est inférieur à celui de l’autre s’il existe une injection du premier sur le second. Or, ces propriétés ont un sens pour les ensembles infinis ! Elles permettent de définir les notions d’inégalité de cardinal. On dira que le cardinal a de M est inférieur à celui b de N (et on notera a ≤ b) s’il existe une injection de M dans N.
Pour que ceci définisse une relation d’ordre total, il faut montrer que ≤ est réflexive (soit a ≤ a pour tout cardinal a) ; c’est bien le cas puisque l’identité est une bijection de M sur lui-même. Cette relation est clairement transitive, c’est-à-dire que si a ≤ b et b ≤ c alors a ≤ c par composition de deux injections.
Pour avoir un ordre total, il faut montrer en outre que soit a ≤ b, soit b ≤ a, ce qui revient à dire qu’étant donnés deux ensembles M et N, soit il existe une injection de M vers N, soit il en existe une de N vers M. Ce résultat était démontré lorsque Cantor a rédigé son article en 1895.
Il faut enfin justifier l’antisymétrie de la relation, c’est-à-dire que si a ≤ b et b ≤ a, alors a = b. Cela revient à montrer que s’il existe une injection de M dans N et une injection de N dans M alors il existe une bijection entre M et N. Ce résultat manquait à Cantor en 1895 ! Son élève Felix Bernstein en donnera une démonstration en 1897. Cantor s’empresse alors de rééditer son article, complété du chaînon manquant.


