
Aujourd’hui, pour effectuer un calcul élémentaire tel que 128 + 361, on a recours à une calculatrice de base, un smartphone, un ordinateur. L’accès à ces objets n’a pas toujours été possible. Des méthodes de calcul ont été développées pour effectuer une telle tâche « à la main » ; on parle de calcul posé ou de calcul écrit. On présente et on effectue un calcul de la manière suivante :
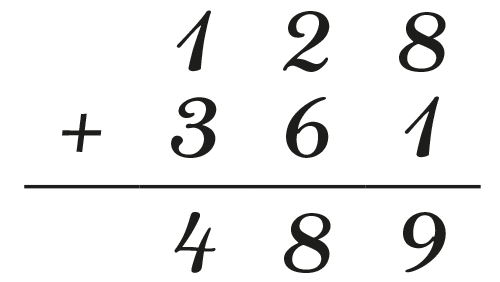
Par « calcul écrit », on entend donc transformer un calcul élaboré en plusieurs calculs plus élémentaires. Dans notre exemple, on transforme une addition de deux nombres à trois chiffres en trois additions de deux nombres à un chiffre. Tout cela avec une présentation écrite pour nous faciliter les choses et ne pas simplement faire du calcul mental.
Pas de technique universelle
Développer des techniques de calcul semble universel. Mais, historiquement, tout le monde disposait-il des mêmes techniques ? Celles que nous utilisons aujourd’hui sont-elles les plus pratiques ? La réponse est doublement non.
Déjà, nous utilisons un système de numération de position. L’écriture du nombre 361 encode l’information que l’on a trois centaines, six dizaines et une unité. Le « 3 » représente des centaines car il est en troisième position à partir de la droite. Le même nombre, 361, en écriture romaine s’exprime sous la forme CCCLXI. Le « L » représente 50 non pas parce qu’il est dans une position particulière dans l’écriture, mais simplement parce que c’est le caractère utilisé pour désigner 50.
L’habitude a été prise d’écrire les chiffres romains dans un certain ordre.
Ce n’est pas absolument nécessaire : on pourrait tout aussi bien écrire « CLCXIC » pour « 361 » (soir 100 + 50 + 100 + 10 + 1 + a;100). Ce n’est que l’écriture tardive du nombre 4 par IV plutôt que IIII qui interdira de modifier l’ordre des chiffres romains !
Les utilisateurs des chiffres romains avaient des techniques de calcul qui leur étaient propres. Ils calculaient avec des abaques (voir article « Calculer ? Avec des calculi, évidemment ! »). L’ouvrage de Fibonacci popularisant les chiffres indo-arabes en Europe datant de 1202 s’appelle d’ailleurs Liber abaci, littéralement « livre des abaques ».
Si l’on se concentre sur la numération de position, les techniques de calcul écrit sont basées sur les mêmes principes pour l’addition et pour la soustraction. Une différence subsiste encore aujourd’hui dans l’enseignement pour la soustraction.
En effet, si l’on doit effectuer l’opération 361 − 128, il semble que l’on doive ôter huit unités d’une unité. La plupart des enseignants préconisent la méthode de l’emprunt ; d’autres préfèrent la méthode de la compensation.
L’emprunt consiste à ôter une dizaine du premier nombre pour la remplacer par dix unités au même nombre. La compensation consiste à augmenter le premier nombre de dix unités et le second d’une dizaine.
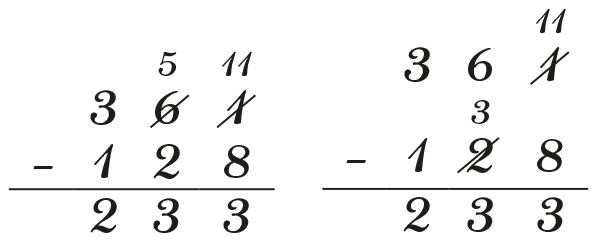
Dans le premier cas, on utilise le fait qu’une dizaine équivaut à dix unités, et dans le second qu’en augmentant chaque nombre de la même quantité la différence ne change pas. Ce ne sont pas des techniques propres à l’écriture d’un calcul : les utilisateurs des bouliers procèdent de la même manière !
Une méthode ancienne
Pour la multiplication, une méthode consistant à transformer un calcul élaboré en plusieurs calculs élémentaires se trouve sur le papyrus Rhind. Son auteur, le scribe Ahmès, au XVIe siècle avant notre ère, précise qu’il rédige une copie d’un autre papyrus confectionné trois siècles plus tôt. Sur ce papyrus se trouve la multiplication égyptienne. Le principe de base est qu’il suffit d’être capable de multiplier les nombres par 2 et d’additionner. Ainsi, si l’on veut multiplier le nombre 45 par 51, on part du nombre 45, que l’on multiplie encore et encore par 2, sans dépasser une multiplication par 51.

Les astérisques dans la colonne de droite permettent de reconstituer le nombre 51 (en effet, 51 = 1 + 2 + 16 + 32).
Pour obtenir le résultat final, il suffit d’additionner les nombres correspondants dans la colonne de gauche : 45 × 51 = 45 + 90 + 720 + 1 440. La multiplication par 51 a ainsi été transformée en plusieurs multiplications par 2 et quelques additions.
Il suffit donc d’être capable de multiplier un nombre par 2 pour pouvoir multiplier un nombre par n’importe quel autre nombre. Se cache finalement, derrière cette méthode, l’écriture binaire d’un nombre (son écriture comme somme de puissances de 2) utilisée en informatique. Une méthode semblable a été enseignée en Russie encore à la fin du XIXe siècle.
Face à la multiplication égyptienne, on pourrait penser que la méthode que nous apprenons à l’école primaire est « plus facile ». Mais comment mesurer la « facilité » d’un algorithme ? Les méthodes actuelles sont-elles la conclusion de méthodes « de plus en plus faciles à appliquer » ? Étonnamment, non ! Voici une multiplication actuelle.
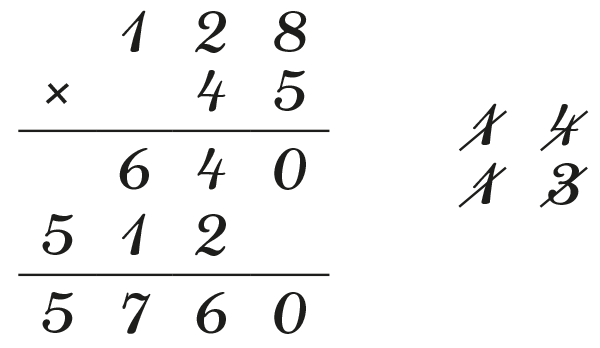
La grande difficulté dans l’apprentissage de cette méthode réside dans les reports multiplicatifs à droite. Il faut d’abord les effectuer en les notant, puis les exploiter à l’étape suivante en les barrant pour indiquer qu’on les a utilisés. La difficulté principale, outre le décalage de 512 par rapport à 640, se situe dans ces reports. Pourtant, auparavant, des méthodes existaient pour s’en passer. Lorsqu’il effectuait une multiplication, le mathématicien français Jean Baptiste Joseph Fourier (1768‒1830) n’en avait pas ; il passait à la ligne à chaque multiplication (voir exemple ci-contre) ! La seule difficulté subsistant était celle du « décalage », néanmoins accentuée par le nombre de lignes composant la partie intermédiaire.
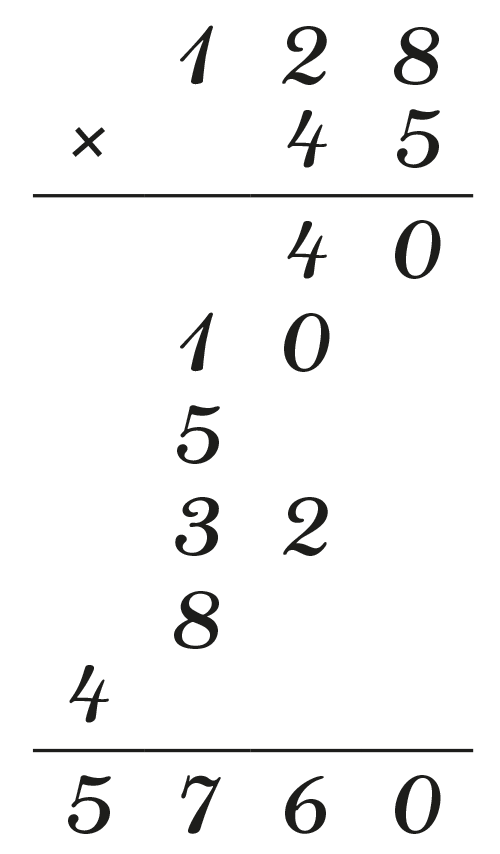
Que dire aussi de l’espace utilisé ? Pour multiplier un nombre à trois chiffres par un nombre à deux chiffres, on utilise 3 × 2 lignes intermédiaires. En imaginant multiplier un nombre à cinq chiffres par un nombre à quatre chiffres et les vingt lignes correspondantes, on comprend pourquoi on enseigne les reports multiplicatifs…
Des représentations plus compactes
Heureusement, il existe une méthode à la fois plus compacte et sans report multiplicatif ; elle est même plus ancienne. Elle se trouve dans le Liber abaci ainsi que dans des manuscrits arabes du Xe siècle ; elle pourrait même avoir été connue plus tôt des mathématiciens indiens.
Pour multiplier un nombre à trois chiffres par un nombre à deux chiffres, on crée une grille 3 × 2. Les chiffres du premier nombre indicent les colonnes ; ceux du second indicent les lignes. La multiplication 128 × 45 donne ainsi la grille suivante.

On trace ensuite des diagonales de chaque case et on effectue les multiplications, comme dans un tableau à double entrée. La dizaine est inscrite « en haut, à gauche » et l’unité « en bas, à droite ». On retrouve dans les six cases les six lignes de la méthode de Fourier, mais de manière plus compacte.

Les diagonales font penser à un rideau en jalousie, très prisé en Toscane à la Renaissance, donnant cette appellation per gelosia, comme pour les volets « en jalousie » (en français) qui permettent de regarder, voire espionner, ce qui se passe à l’extérieur… sans être vu.
Les diagonales dessinent une troisième direction dans ce tableau ; on les utilise de manière additive, de droite à gauche. Le résultat est indiqué en fin de diagonale, en utilisant les inévitables reports additifs.

Le résultat final apparait alors « en bas, à gauche » du tableau : 5 760.
Alors pourquoi une méthode à la fois compacte et sans report multiplicatif n’est-elle pas utilisée aujourd’hui ? Une explication réside dans la popularisation de l’utilisation de l’encre : à l’époque où l’encre n’est pas effaçable et nécessite des buvards, la réalisation d’une telle grille est évidemment problématique, ne serait-ce que pour réaliser toutes les lignes à l’encre sans laisser de traces !
Les divisions sont le domaine où les techniques varient beaucoup plus. Dans son ouvrage posthume publié en 1736, le mathématicien François Barrême (1638‒1703) recense plusieurs techniques : à la française, à l’italienne longue, à l’italienne courte, à l’espagnole et à la portugaise, la persienne ou l’indienne. En réalité, toutes ont la présentation à la galère, excepté l’italienne. À l’époque les opérations s’effectuaient à droite et le résultat se notait à gauche. La présentation moderne de la division est en réalité la division à l’italienne. Les autres types de division diffèrent par la technique, mais sont semblables par la présentation dite à la galère.

Le mystère de la galère
Analysons la division « à la galère » de 123 456 par 528. On écrit « 123 456 » au-dessus d’une ligne, et « 528 » en dessous de « 1234 » car il rentre dans 1 234, mais pas dans 123. Il y rentre deux fois ; on inscrit donc 2 à droite de 123 456.
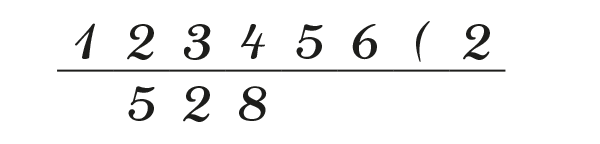
Comme 2×5 = 10, on soustrait cela de 12, ce qui donne 2.
Puis 2 × 2 = 4, ce qui conduit à 19 après soustraction de 23. Ensuite, 2 × 8 = 16, et
194 ‒ 16 = 178.

Le nombre au-dessus de la barre horizontale commence par « 1785 », dans lequel le nombre 528 rentre trois fois. Une procédure similaire conduit à la série d’opérations suivantes.
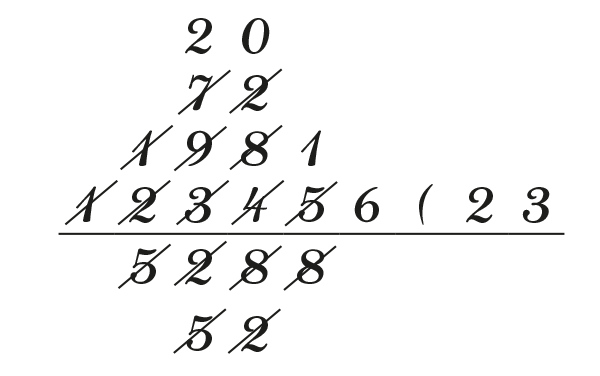
Enfin, dans 2 016, le nombre 528 rentre trois fois.
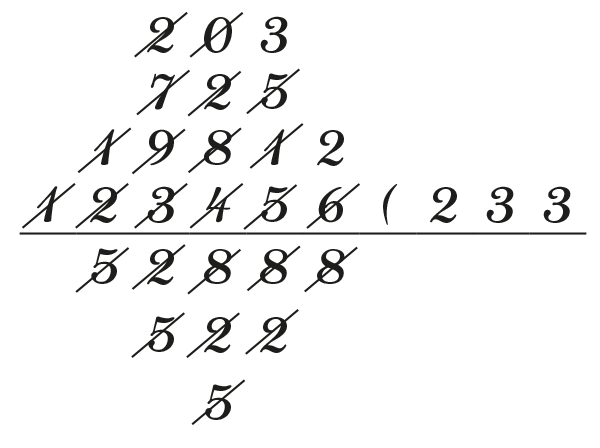
Mais pourquoi une « galère » alors ? L’enseignant de l’époque disait-il que l’élève ne pouvait dessiner les bateaux qu’une fois la liste d’exercices finie ? Pourquoi une galère et pas un autre type de bateau ? Le mystère reste entier !

Un défi à relever
Le calcul écrit peut-il donner lieu à des défis plus poussés ? En 2014, l’Olympiade mathématique belge proposa le problème suivant aux élèves âgés de 12 à 13 ans.
« Nicole a effectué une division écrite au crayon. Pour l’ennuyer, Jules gomme grossièrement quelques chiffres et les remplace par des lettres. Ci-contre se trouve l’opération ainsi maltraitée.
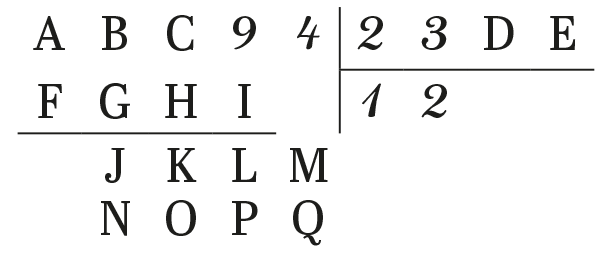
1. Le chiffre des unités du diviseur peut-il être 3 ? 6 ?
2. Quel aurait pu être le calcul de Nicole ? Justifier chaque remplacement de lettre par un chiffre. S’il y a plusieurs solutions, envisager toutes les possibilités. »
Si le jury de l’Olympiade s’attendait à une justification lettre par lettre, un jeune participant, Nicolas Beyne, bouleversa cette idée en renversant complètement le problème. Le dividende D est égal au diviseur d multiplié par le quotient q augmenté du reste r (autrement formulé, on a D = dq + r).
Ainsi, ABC94 = 23DE × 12 + 30, ou ABC64 = 23DE × 12.
Dès lors, 2 300 × 12 ≤ ABC64 ≤ 2 399 × 12, ou 27 600 ≤ ABC64 ≤ 28 788.
Ainsi, A = 2 et, le nombre 2BC64 commençant par 27 ou 28 et étant divisible par 12 et donc par 3, il est égal à 27 864, 28 164, 28 464 ou 28 764. Il suffit alors d’effectuer les quatre divisions pour se rendre compte qu’il y a quatre solutions. Nicolas Beyne a reçu le prix d’élégance, ce qui est assez rare pour un élève de cet âge !
Le problème suivant a été refusé, car considéré comme trop compliqué pour des élèves de cet âge-là :

Pourtant, contrairement au précédent, et étrangement au vu de la faible quantité de chiffres fournie, la solution est unique ! Pourrez-vous relever ce défi ?
Michel Sebille enseigne à l’École européenne d’Ixelles (Belgique).


