Il existe de nombreuses méthodes pour construire des ellipses « à la main » : avec une règle plate, ou un triangle en carton… En effet, le lieu géométrique d'un point appartenant à un segment de droite dont les deux extrémités se déplacent sur des droites sécantes est toujours une ellipse, éventuellement aplatie. Cette propriété est utilisée dans la construction dite « à la bande de papier ». Ici, la bande de papier est remplacée par une simple règle plate, rigide et graduée.
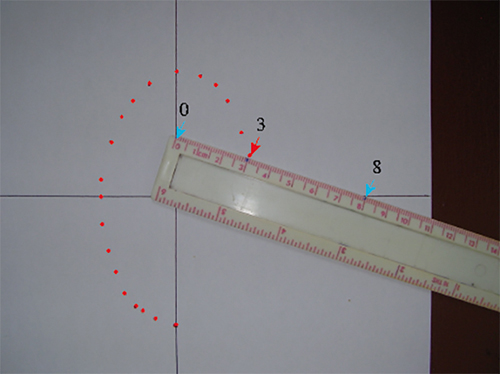
On déplace simultanément le point « 0 » de la règle sur l'axe vertical et le point « 8 » sur l'axe horizontal et l'on marque les positions successives du point « 3 ». On obtient une belle ellipse de demi-grand axe 5 cm et de demi-petit axe 3 cm.
1. Sauriez-vous justifier que la courbe obtenue est bien une ellipse ?
Il existe des mécanismes basés sur un principe similaire. Le philosophe grec Proclus (412-485) décrit un tel système dans ses Commentaires sur Euclide. On trouve de tels ellipsographes dans le commerce, proposés parmi les jouets pour enfants.

Un ellipsographe basé sur le principe décrit par Proclus :
deux points du bras noir coulissent sur des axes perpendiculaires,
le crayon étant fixé dans le tube rouge.
La construction précédente utilise deux axes orthogonaux, mais la construction reste valable (et la courbe résultante demeure une ellipse) avec deux axes sécants formant un angle quelconque.

La construction suivante, dont les précédentes sont des cas particuliers, est due à Frans van Schooten (1615-1660), mathématicien néerlandais qui consacra un livre aux mécanismes permettant de tracer des coniques. Dans son ouvrage Exercitationes mathematicae (1657), il propose le problème suivant : « Déterminer le lieu géométrique décrit par le troisième sommet d'un triangle lorsque les deux premiers se déplacent respectivement sur deux droites sécantes. »
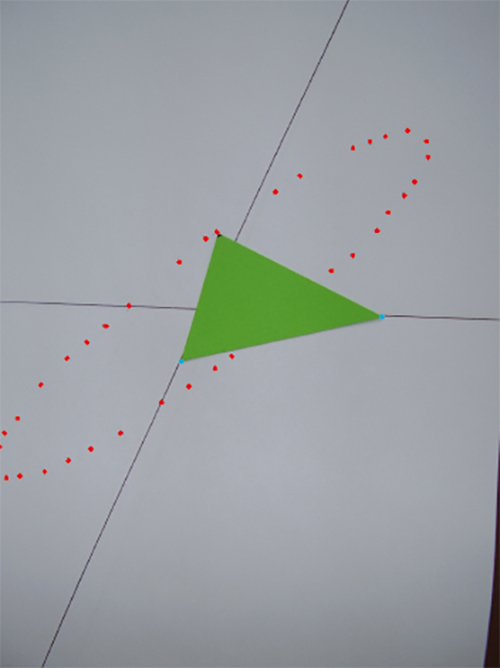
En utilisant un triangle quelconque réalisé en carton fort, on fait glisser simultanément deux sommets de ce triangle (en bleu sur l'image) sur les deux axes du repère, et on marque les positions successives du troisième sommet. Le lieu géométrique de ces positions est à nouveau une ellipse !
2. En admettant la propriété dans le cas de deux axes perpendiculaires, démontrez que c'est encore vrai avec deux axes obliques.
SOURCES
Site Internet Mathcurve, https://www.mathcurve.com/ 100 Great Problems of Elementary Mathematics. Heinrich Dörrie, Dover, 1965.

