Des cinq polyèdres réguliers, un seul permet de paver l'espace ; il s'agit du cube, bien sûr. Mais est-il possible de paver l'espace, sans laisser de vides, avec une combinaison de deux ou plusieurs polyèdres réguliers ? Étonnamment, oui. Voici la recette d'un « pavage semi-régulier » de l'espace.

L'idée consiste, pour paver l'espace, sans trous, à utiliser des octaèdres réguliers et des tétraèdres réguliers. Il s'agit d'ailleurs du seul pavage semi-régulier de l'espace.

Commençons par construire une couche d'octaèdres réguliers, ces octaèdres étant disposés comme l'indique la figure, et étant en nombre infini dans les deux directions horizontales.

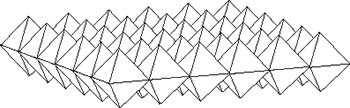
Ensuite, on insère des tétraèdres réguliers dans chaque angle solide formé par deux octaèdres adjacents. Ces tétraèdres apparaissent en bleu sur le dessin.

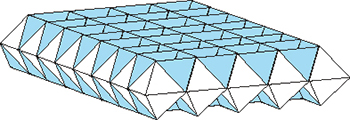
On obtient alors un solide dont les faces du dessous et du dessus sont un peu semblables à des alvéoles de boîtes à œufs. Mais au lieu d'y placer des œufs, insérons une nouvelle couche de tétraèdres dont les pointes vont venir occuper exactement l'espace disponible entre les tétraèdres. On peut ainsi remplir tout l'espace, sans trou, couche après couche.

1. Quel est le rapport du nombre de tétraèdres sur le nombre d'octaèdres ?

Des octaèdres de plus en plus grands

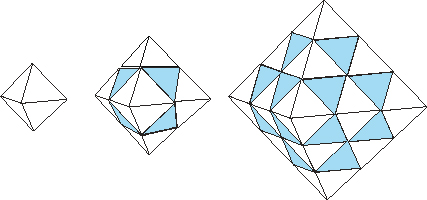
En utilisant cette méthode, construisons des octaèdres pleins de plus en plus grands à partir de petits octaèdres et de petits tétraèdres, toujours réguliers. De gauche à droite, nous avons :

• un octaèdre unique, qui sera notre octaèdre de base ;

• un octaèdre de dimension double du précédent, constitué de six octaèdres de base et de huit tétraèdres de base ;

• un octaèdre de dimension triple du premier, constitué de dix-neuf octaèdres de base et de trente-deux tétraèdres de base.

On pourrait continuer cette suite en construisant des octaèdres d'arêtes 4, puis 5, puis 6… Ces constructions utiliseraient les nombres d'octaèdres et de tétraèdres qui figurent dans le tableau. On constate d'ailleurs que le rapport « nombre de tétraèdres / nombre d'octaèdres » semble tendre vers une limite, ce qui confirmerait la réponse à la question 1 posée plus haut.

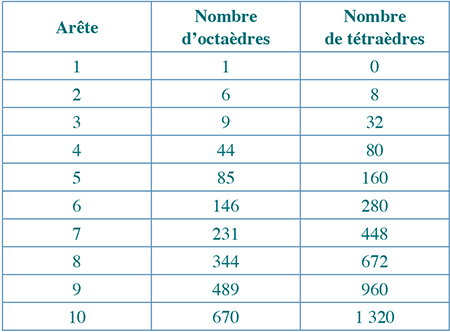
2. Combien d'octaèdres et de tétraèdres nécessiterait la construction d'un octaèdre d'arête n ?