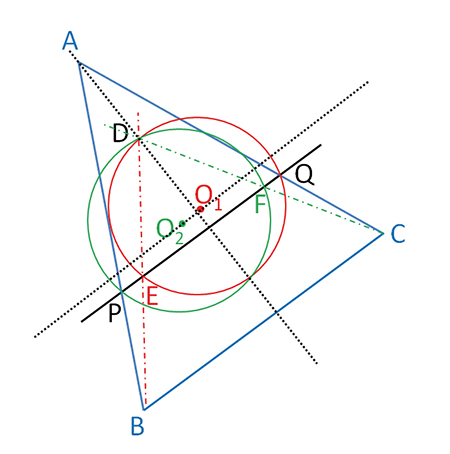
Soit un triangle ABC. On construit P un point de [AB] et Q un point de [AC] tels que la droite (PQ) soit parallèle à (BC). Soit maintenant D un point intérieur au triangle APQ. La droite (BD) coupe (PQ) en E et la droite (CD) coupe (PQ) en F.
Soient maintenant O1 le centre du cercle circonscrit au triangle DEQ et O2 le centre du cercle circonscrit au triangle DFP. Démontrez que (O1O2) est perpendiculaire à (AD).